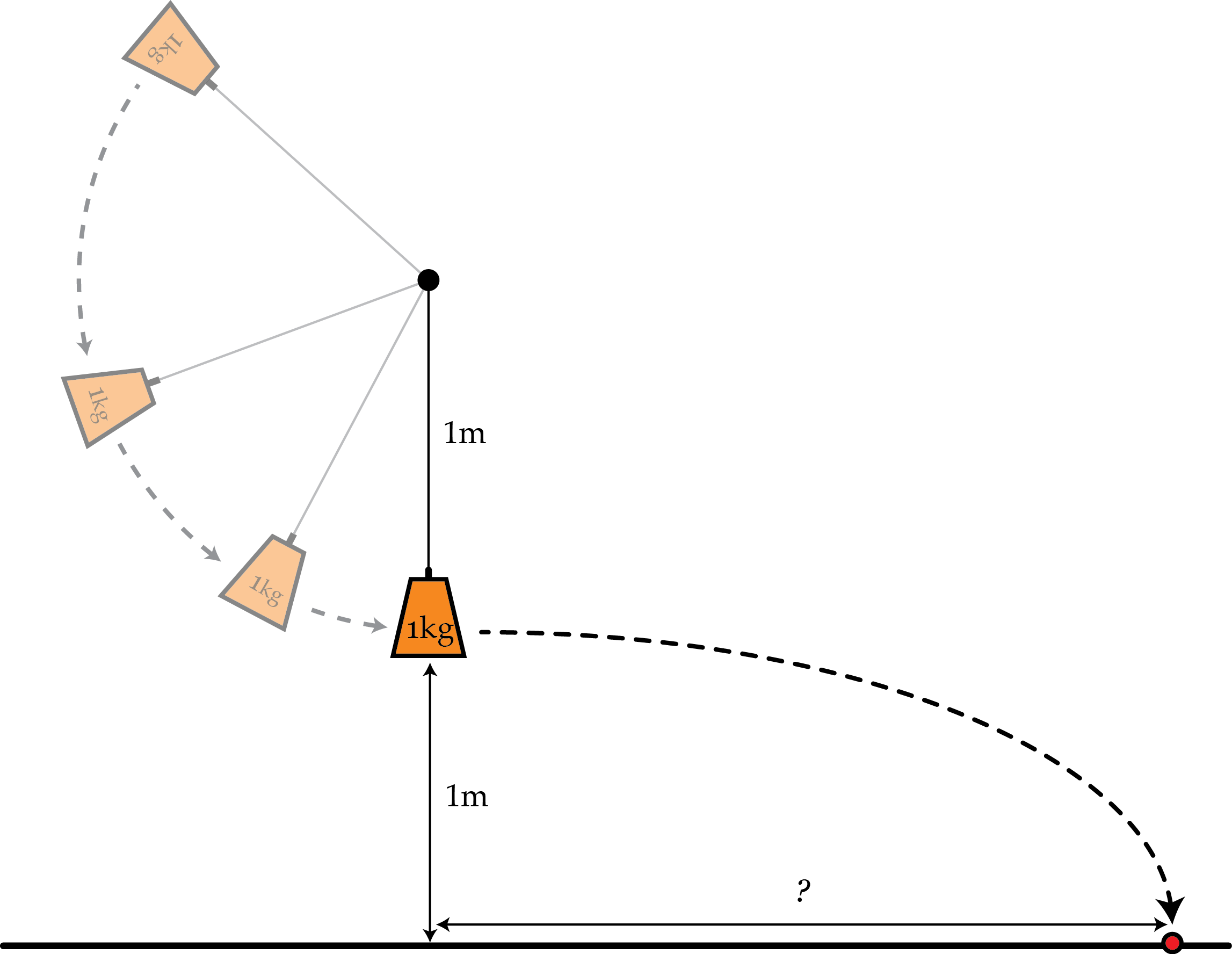
Duck, incoming rock!
You tie a
1
kg
mass to the end of a
1
m
long string. The string has a breaking tension of
2
0
0
N
and you swing it in a vertical circle faster and faster. At the very bottom of one swing the string breaks and the mass flies off horizontally from a height of
1
m
. How far has the mass gone horizontally
in meters
when it hits the ground?
Details and assumptions
- The acceleration of gravity is − 9 . 8 m/s 2 .
The answer is 6.23.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
This solution has the physics correct and no unnecessary steps, which is great. However, keep in mind that being correct is only the first step to success in a technical field. Also key is whether you can explain what's going on to others. Good expository skills are not just for those interested in teaching, they are necessary no matter what profession you go into. Engineering firms want people who can work in teams and communicate their ideas, doctors need to explain medical issues to their patients, and even at the highest levels of academia scientists still communicate via papers and talks. A great idea that you can't explain doesn't do anyone any good.
So, what could be improved in this solution in terms of the exposition? First, when writing an equation, write it symbolically and explain what each symbol in the equation means before plugging in numbers. The sentence quoted below, ``If the velocity of the mass is v m/s then we can write, v^2/1 + 1*9.8=200 v=13.79 m/s'', explains what v is and solves for it properly, which is good. However, where does the equation come from? A clearer exposition would be the following:
If the velocity of the mass is v m/s then, using Newton's second law and the fact that the acceleration is centripetal acceleration, we have F N e t = m a → 2 0 0 N − m g = m r v 2 , where m is the mass of the object and r is the length of the rope. Substituting in m=1 kg and r=1 m allows us to solve for v=13.79 m/s.
A good solution is more valuable than a good answer, so don't shirk the details when writing them!
Before the string breaks, the object undergoes uniform circular motion. To solve for its speed v upon flying off, we analyze the forces on the object at the very bottom of the swing:
Net centripetal force is the tension T on the string less the weight W = m g of the object, i. e. r a d i u s m ⋅ v 2 = T − m g . We substitute the given values to get v = 1 3 . 7 9 m / s .
As the object flies off, the horizontal component of its motion is given by x = v t , or t = x / 1 3 . 7 9 ( ∗ ) , while the vertical component is y = y 0 − g t 2 / 2 , or t 2 = 0 . 2 0 ( ∗ ∗ ) .
Substituting * in ** yields x = 6 . 2 3 m .
Right before the string breaks, the net force keeping the mass moving in a circle is F N e t = 2 0 0 − ( 1 ) ( 9 . 8 ) = 1 9 0 . 2 N . This is equal to the mass times the centripetal acceleration, i.e. 1 9 0 . 2 = m v 2 / r which can be solved for v = 1 3 . 7 9 m/s . The mass goes into projectile motion after the string breaks, with an initial height of 1 m , and an initial horizontal velocity of 1 3 . 7 9 m/s . It takes the mass 0 . 4 5 seconds to fall 1 m from rest, and so the horizontal distance traveled is x = 1 3 . 7 9 × 0 . 4 5 = 6 . 2 3 m .
At the bottom, the total force acting on the rope is 200N. If the velocity of the mass is v m/s then we can write, v^2/1 + 1 9.8=200 v=13.79 m/s Now it takes \sqrt(2 1/9.8)= 0.45 seconds for the mass to fall vertically by 1 meter as it is having no vertical component of velocity. Thus it covers 13.79*0.45 meters = 6.23 meters horizontally before touching the ground.