Dynamic Geometry: P13
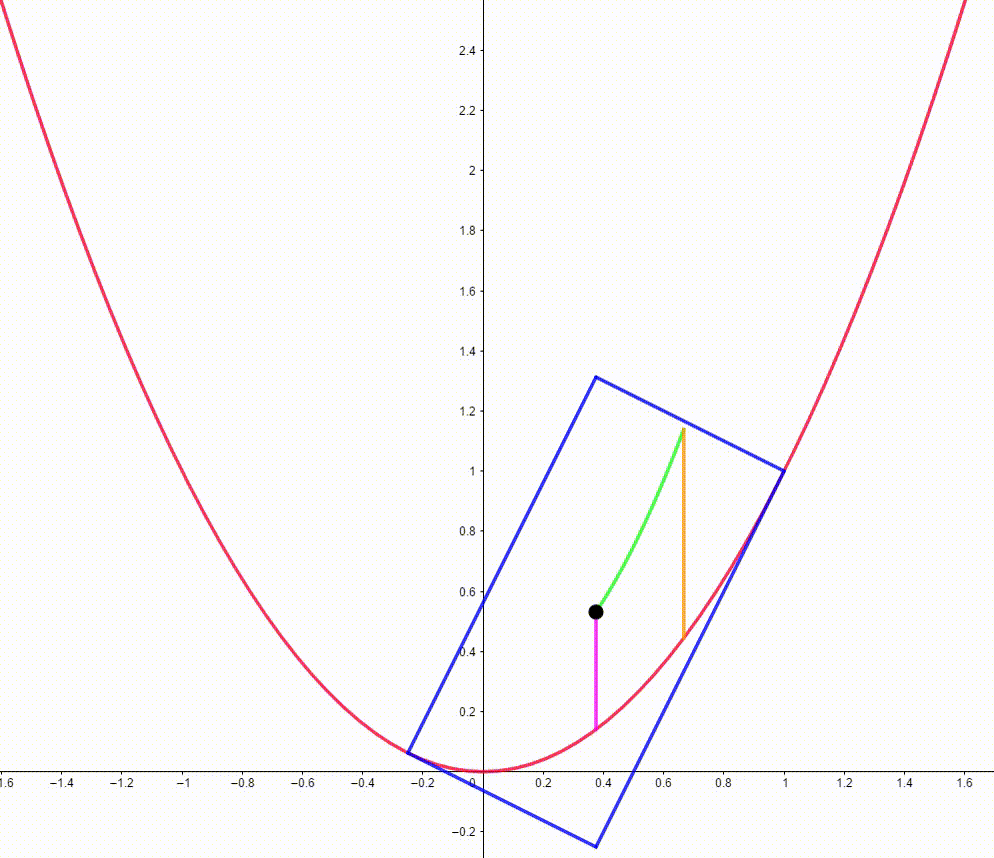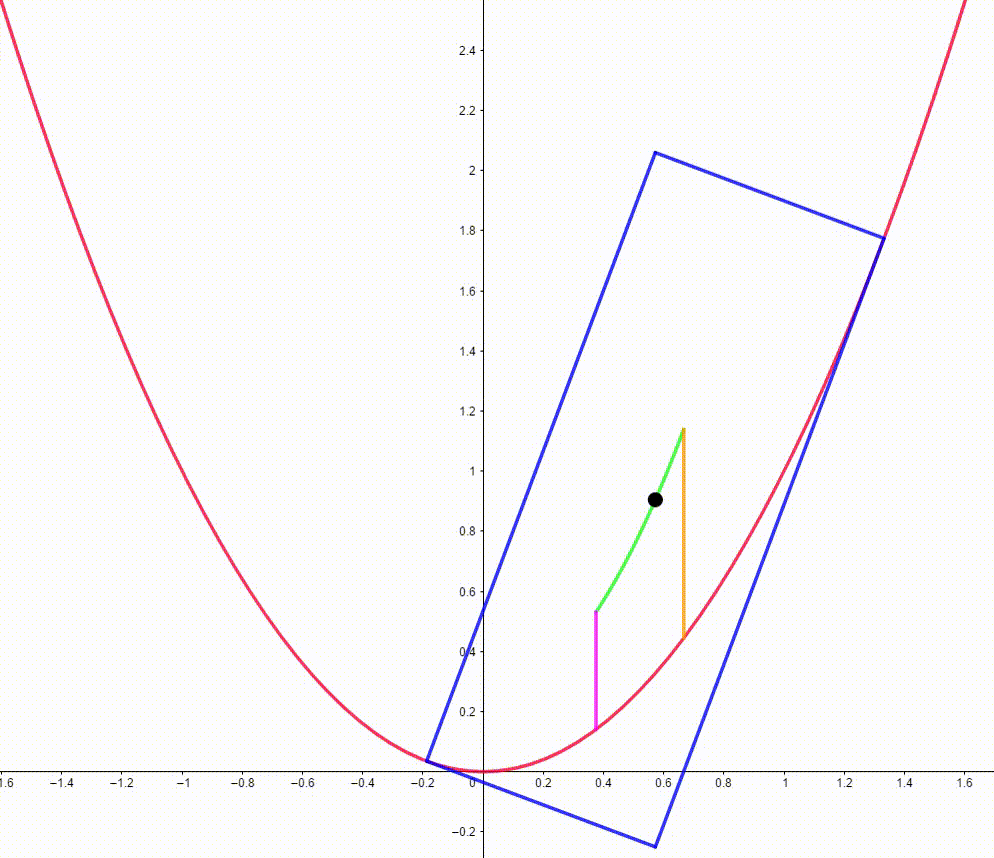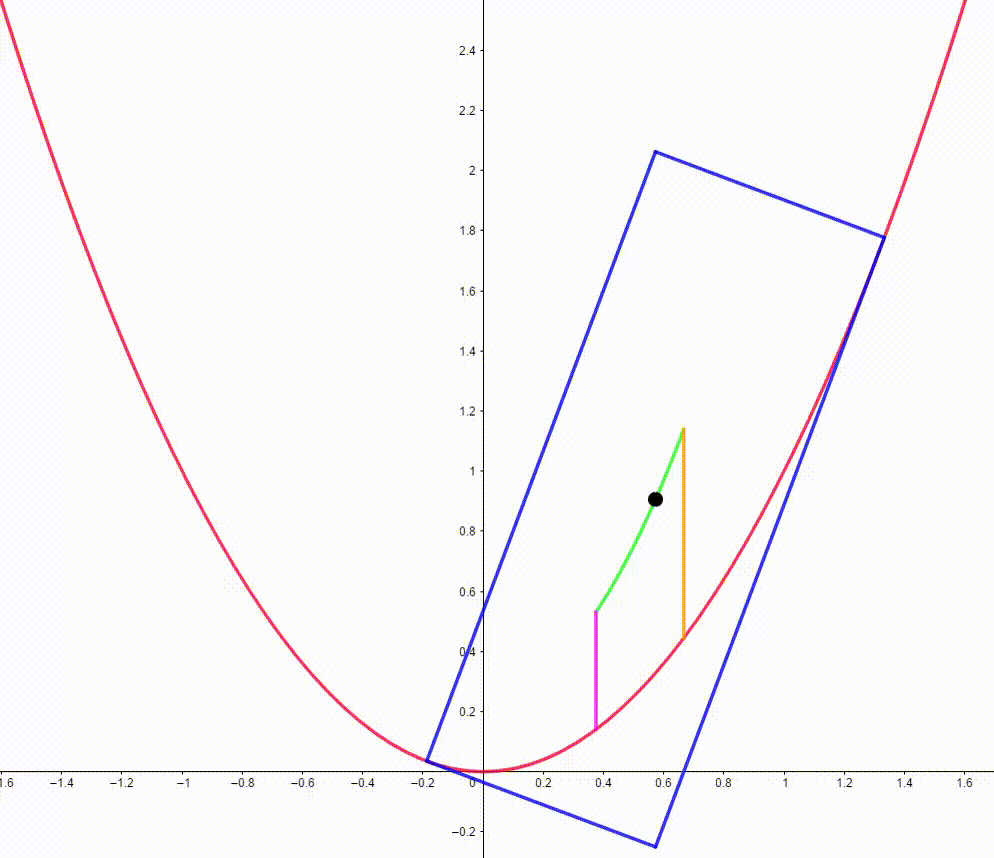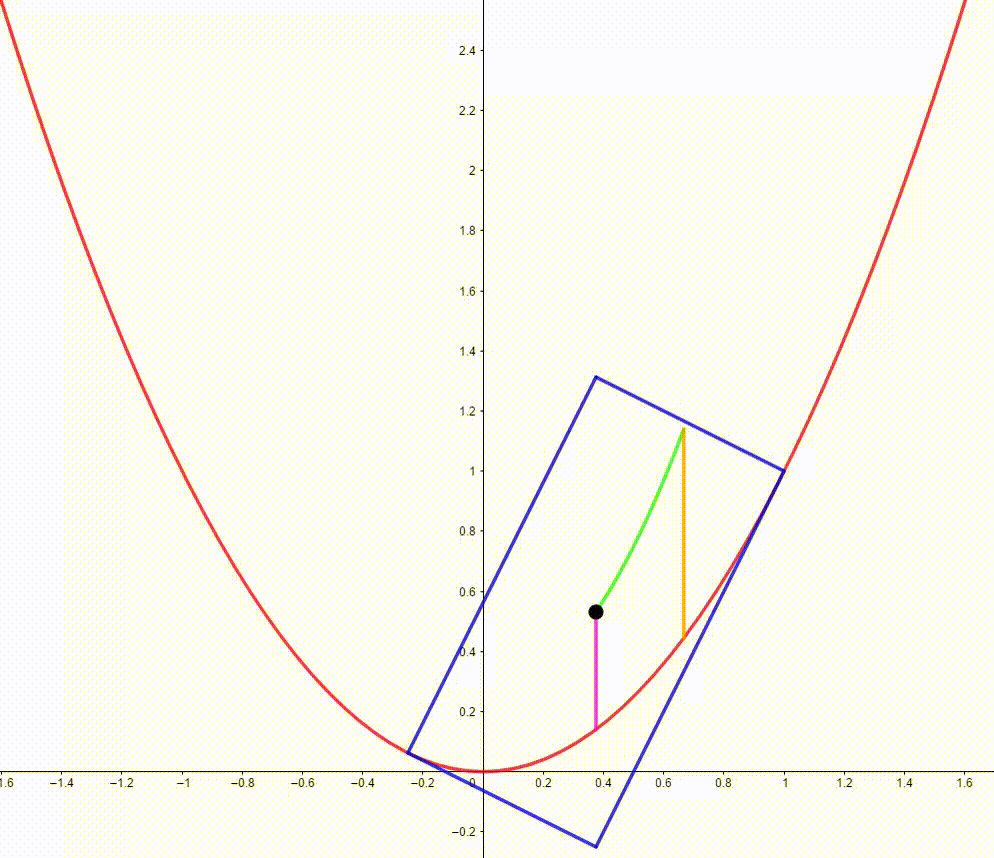 The diagram shows a red parabola
. We place two points on the parabola such that their tangents to the parabola and normals form a blue rectangle. The black point is the center of the blue rectangle and moves along a green curve. It bounces between to vertical segments. When the black point touches the pink segment, the area of the rectangle is equal to
. When the black point touches the orange segment, the area of the rectangle is equal to
. The area bounded by the green curve, the parabola, the pink vertical segment and the orange vertical segment can be expressed as
where
and
are coprime positive integers. Find
.
The diagram shows a red parabola
. We place two points on the parabola such that their tangents to the parabola and normals form a blue rectangle. The black point is the center of the blue rectangle and moves along a green curve. It bounces between to vertical segments. When the black point touches the pink segment, the area of the rectangle is equal to
. When the black point touches the orange segment, the area of the rectangle is equal to
. The area bounded by the green curve, the parabola, the pink vertical segment and the orange vertical segment can be expressed as
where
and
are coprime positive integers. Find
.
The answer is 35081.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Label the diagram as follows, and let the coordinates of P be ( p , p 2 ) and R be ( r , r 2 ) .
Then the tangent line through P is y = 2 p x − p 2 and the tangent line through R is y = 2 r x − r 2 .
As sides of a rectangle, the two tangent lines must be perpendicular, so 2 p ⋅ 2 r = − 1 , or r = − 4 p 1 . Therefore, the coordinates of R are ( − 4 p 1 , 1 6 p 2 1 ) and the tangent line through R is y = − 2 p 1 x − 1 6 p 2 1 .
The coordinates of the intersection of the two tangent lines at S is then ( 8 p 4 p 2 − 1 , − 4 1 ) .
By the distance equation, P S = 8 p ( 4 p 2 + 1 ) 3 and R S = 1 6 p 2 ( 4 p 2 + 1 ) 3 .
The area of the rectangle is then A P Q R S = P S ⋅ R S = 8 p ( 4 p 2 + 1 ) 3 ⋅ 1 6 p 2 ( 4 p 2 + 1 ) 3 = 1 2 8 p 3 ( 4 p 2 + 1 ) 3 .
The center M of the rectangle is the midpoint between P and R , so its coordinates are ( 8 p 4 p 2 − 1 , 3 2 p 2 1 6 p 4 + 1 ) .
When the area of the rectangle is 1 2 8 p 3 ( 4 p 2 + 1 ) 3 = 1 2 8 1 2 5 , p = 1 , which means M is at ( 8 3 , 3 2 1 7 ) on the pink segment, and when the area of the rectangle is 1 2 8 p 3 ( 4 p 2 + 1 ) 3 = 5 4 1 2 5 , p = 2 3 , which means M is at ( 3 2 , 3 6 4 1 ) on the orange segment.
Since x = 8 p 4 p 2 − 1 can be rearranged to p = x + 2 1 4 x 2 + 1 , the locus of points for M is y = 3 2 ( x + 2 1 4 x 2 + 1 ) 2 1 6 ( x + 2 1 4 x 2 + 1 ) 4 + 1 = 2 x 2 + 4 1 .
Therefore, the bounded area is A = ∫ 8 3 3 2 ( 2 x 2 + 4 1 − x 2 ) d x = 4 1 4 7 2 6 3 9 1 , so that a = 6 3 9 1 , b = 4 1 4 7 2 , and b − a = 3 5 0 8 1 .