Dynamic Geometry: P6
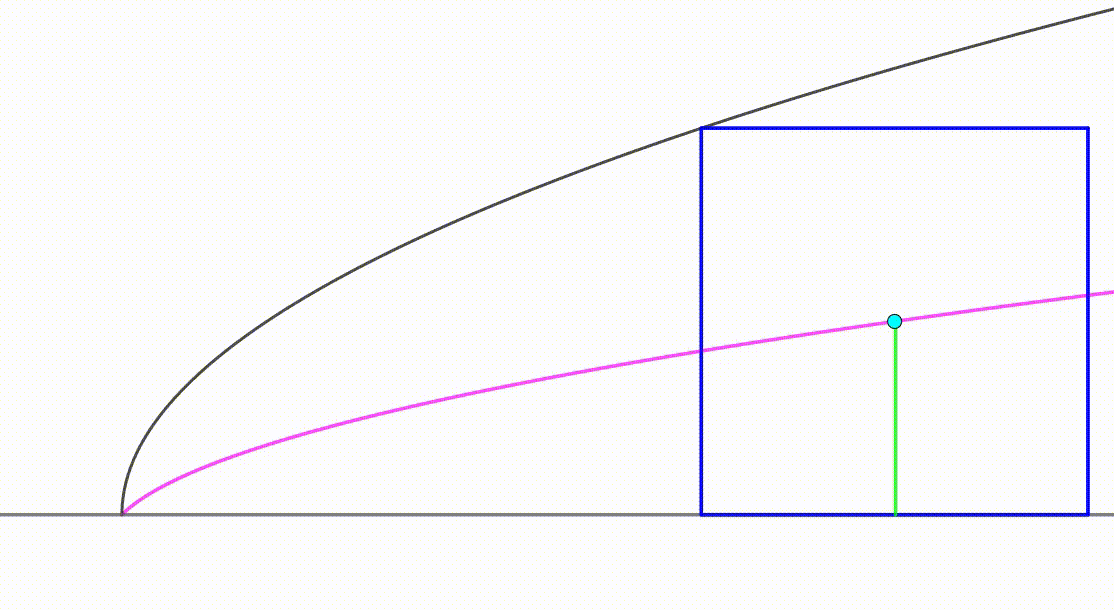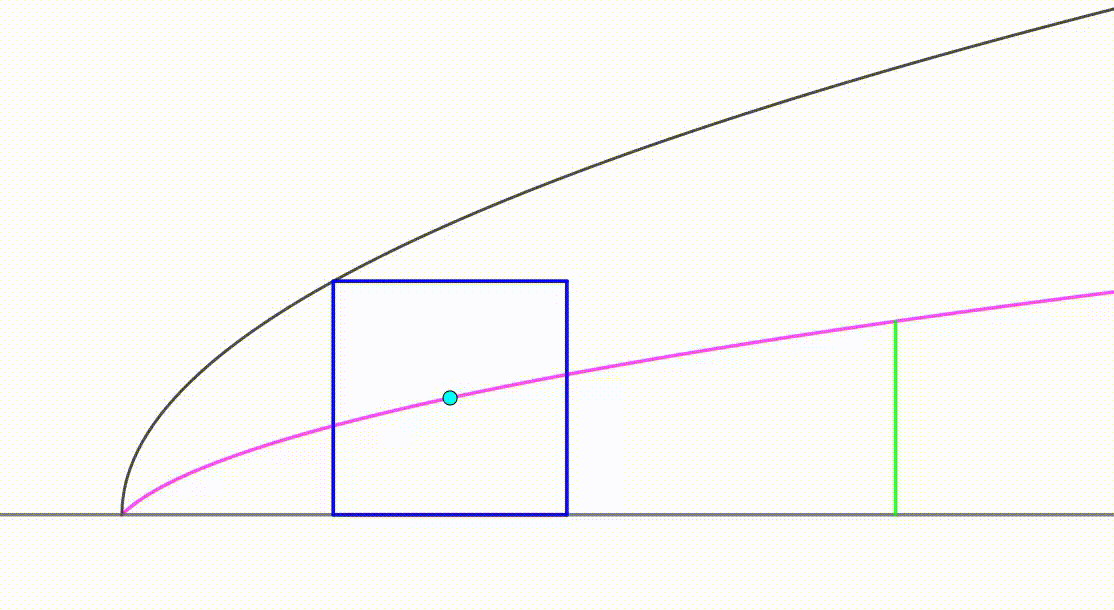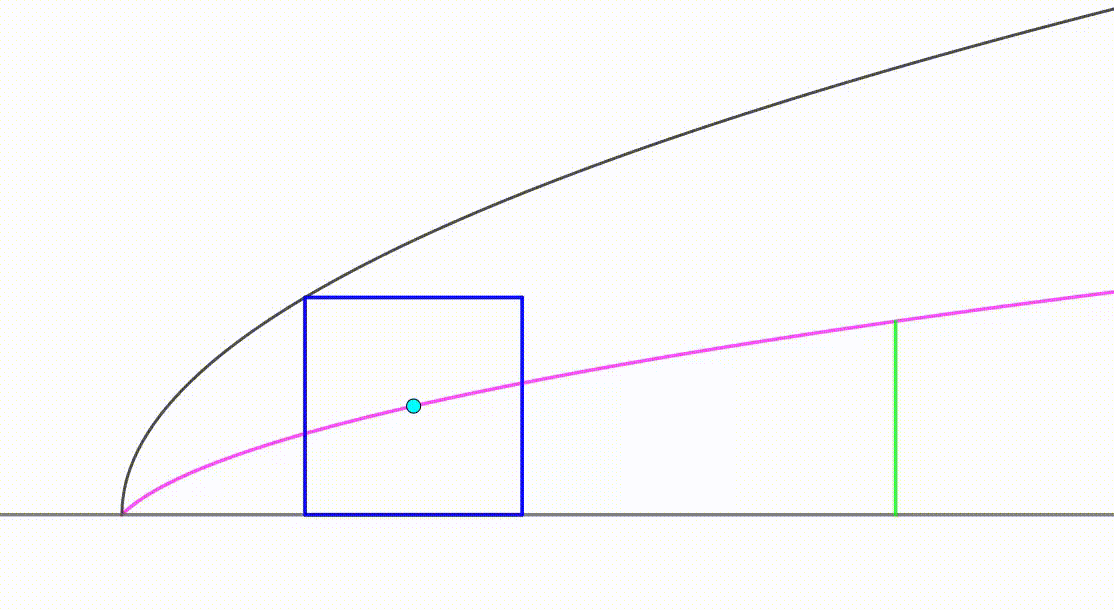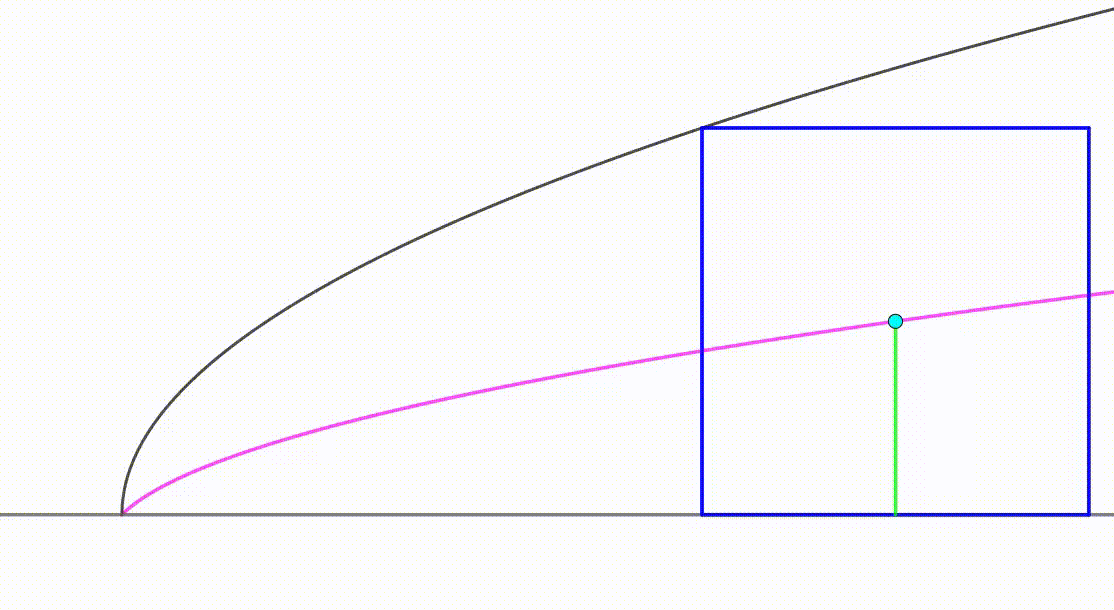 The diagram shows a black curve
and a blue square moving so that it's tangent to the curve and to the line
. As the square is moving, its center (cyan) is following the path of a pink curve from the origin to a green vertical segment. When the center touches the green segment, the area of the square is equal to
. The area bounded by the pink curve, the green segment and the line
can be expressed as
where
and
are coprime positive integers. Find
.
The diagram shows a black curve
and a blue square moving so that it's tangent to the curve and to the line
. As the square is moving, its center (cyan) is following the path of a pink curve from the origin to a green vertical segment. When the center touches the green segment, the area of the square is equal to
. The area bounded by the pink curve, the green segment and the line
can be expressed as
where
and
are coprime positive integers. Find
.
The answer is 77.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the point A that represents the bottom-left angle of the square be ( k , 0 ) . Then the coordinates of the cyan point is ( k + 2 k , 2 k ) . When the cyan point touches the green segment, S □ = 4 9 , implying ( k ) 2 = 4 9 . This solves to k = 4 9 . The integral is therefore S I = ∫ k = 0 k = 4 9 y d x = ∫ 0 4 9 y d k d x d k = ∫ 0 4 9 2 k ( 1 + 4 k 1 ) = ∫ 0 4 9 2 k + 8 1 = 3 1 k 2 3 + 8 1 k ∣ ∣ ∣ ∣ 0 4 9 = 3 2 4 5 .
Hence we input 4 5 + 3 2 = 7 7 as the solution.