Dynamic Geometry: P101
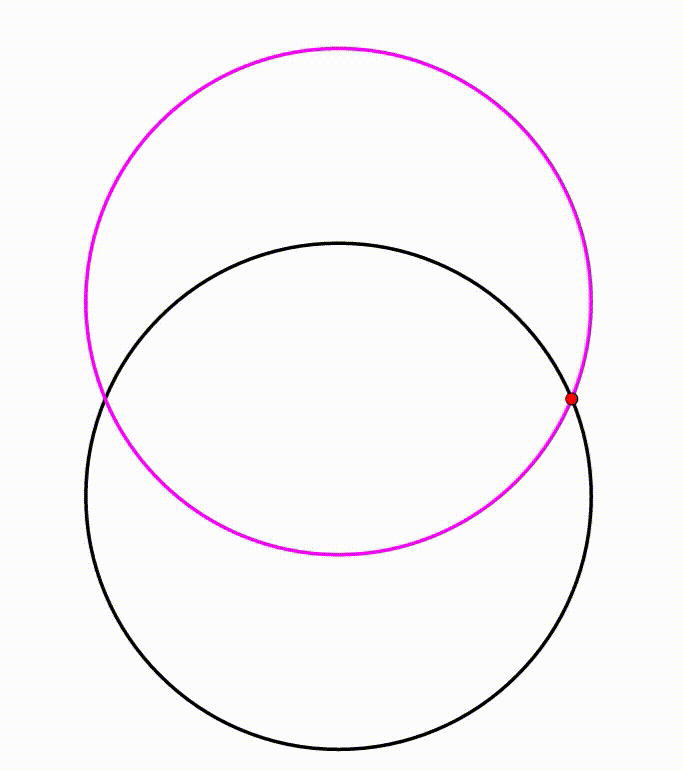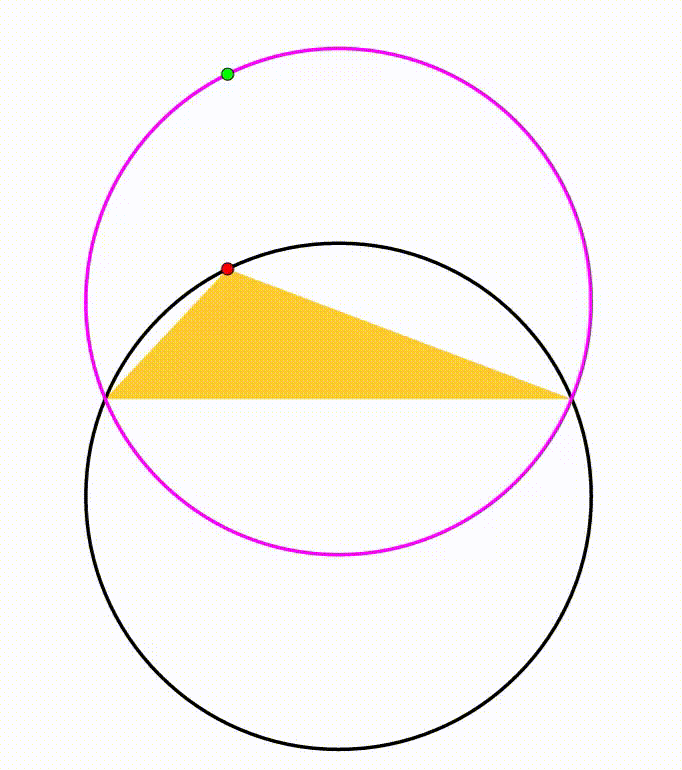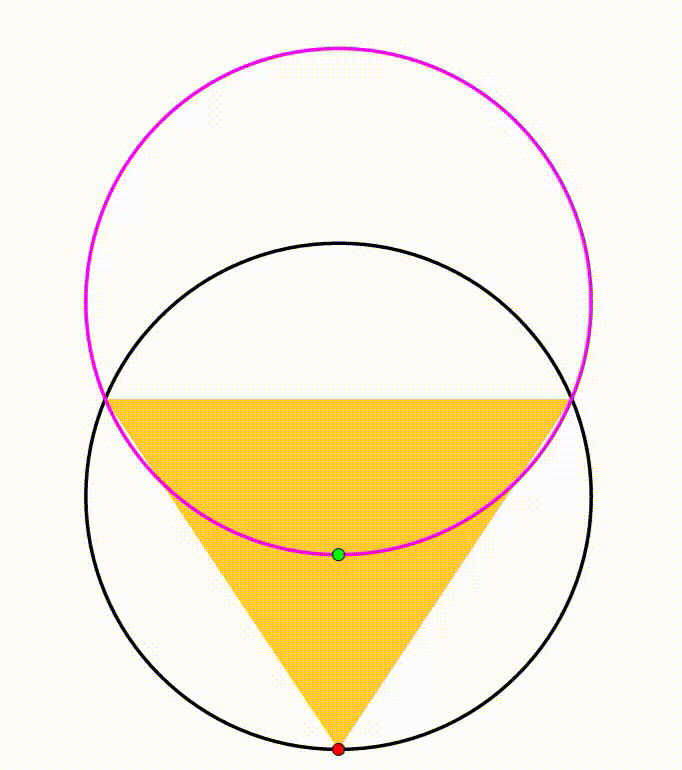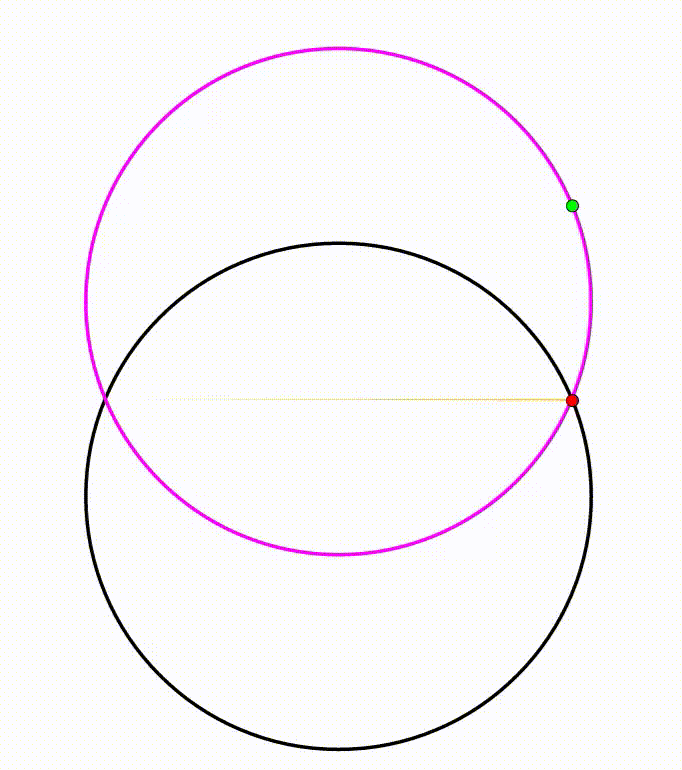 The diagram shows a black circle. A horizontal yellow chord is drawn, creating two circular segments, their respective heights are
4
and
9
. The red point moves freely along the black circle. We use this chord and the red point to draw the yellow triangle. The triangle's orthocenter (green point) traces a
locus
(purple curve). The area bounded by the purple curve can be expressed as
q
p
π
, where
p
and
q
are coprime positive integers. Find
p
−
q
.
The diagram shows a black circle. A horizontal yellow chord is drawn, creating two circular segments, their respective heights are
4
and
9
. The red point moves freely along the black circle. We use this chord and the red point to draw the yellow triangle. The triangle's orthocenter (green point) traces a
locus
(purple curve). The area bounded by the purple curve can be expressed as
q
p
π
, where
p
and
q
are coprime positive integers. Find
p
−
q
.
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
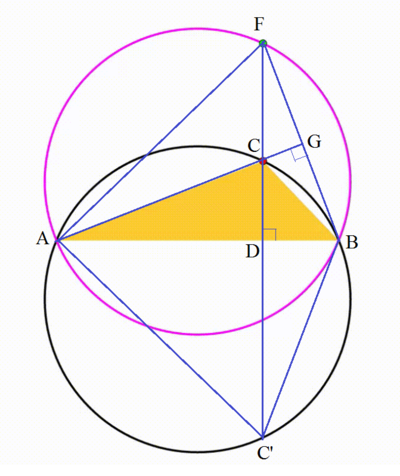
Let the yellow triangle inscribed by the given circle be A B C , where A B is the horizontal dividing chord and C an arbitrary point on the circumference of the circle. Let C D be the altitude from C to A B . Then the orthocenter F of △ A B C is colinear with C and D . Extend A C to meet B F at G . Since F is the orthocenter, A G is perpendicular to B F . Then ∠ G A B = ∠ B F D .
Note that A C B C ′ is a cyclic quadrilateral . Then ∠ G A B = ∠ B C ′ D . Therefore ∠ B C ′ D = ∠ B F D and △ B D F and △ B D C ′ are congruent since ∠ B D F = ∠ B D C ′ = 9 0 ∘ and they share B D . Then every point F on the locus is a reflection of point C ′ about A B . Since C ′ traces out a circle of radius 2 1 3 (see calculations in Dynamic Geometry: P96 Series ), the locus of point F is also a circle of radius 2 1 3 or area 2 2 1 3 2 π . Therefore p − q = 1 3 − 2 = 1 1 .
That's better indeed. Thank you.
We can use the property of the orthocenter that its reflection about any side of the triangle lies on the circumcircle of that triangle. No matter where the red point is, the green point's reflection about the yellow chord will always fall on the black circle. By symmetry, the green point and its reflection trace the same curves, so the purple curve is actually a circle symmetric to the black circle about the yellow chord. The diameter of the black circle is 4 + 9 = 1 3 , so its area is 4 1 6 9 π , meaning that p = 1 6 9 , q = 4 and p − q = 1 1