Dynamic Geometry: P106
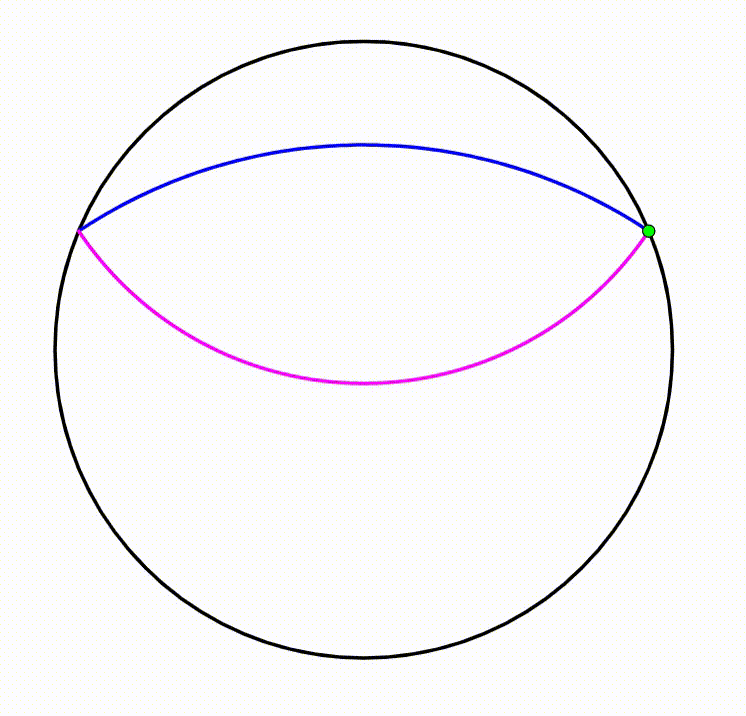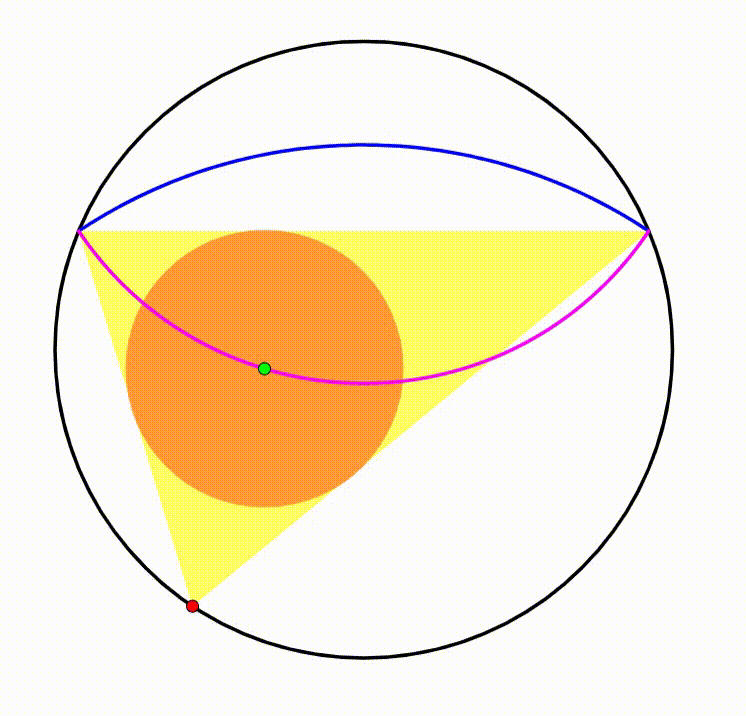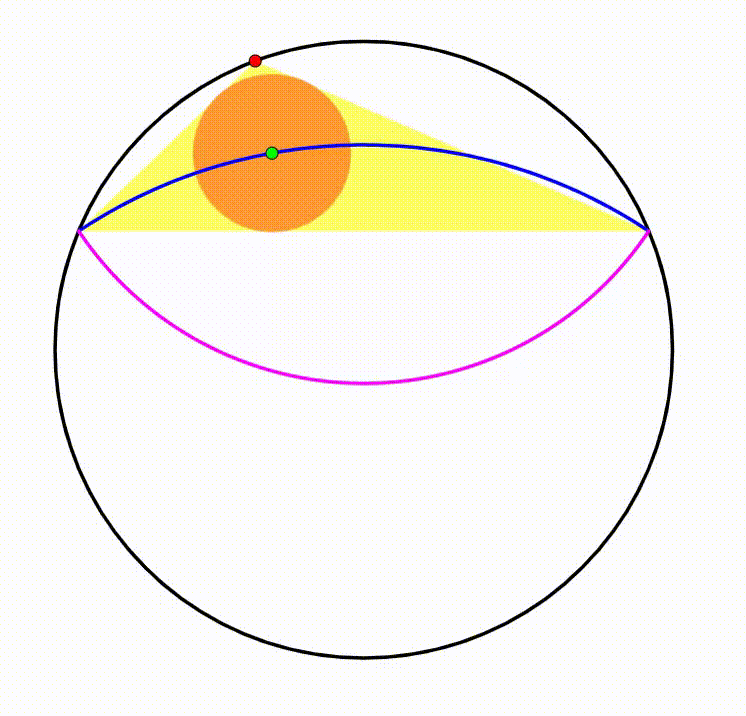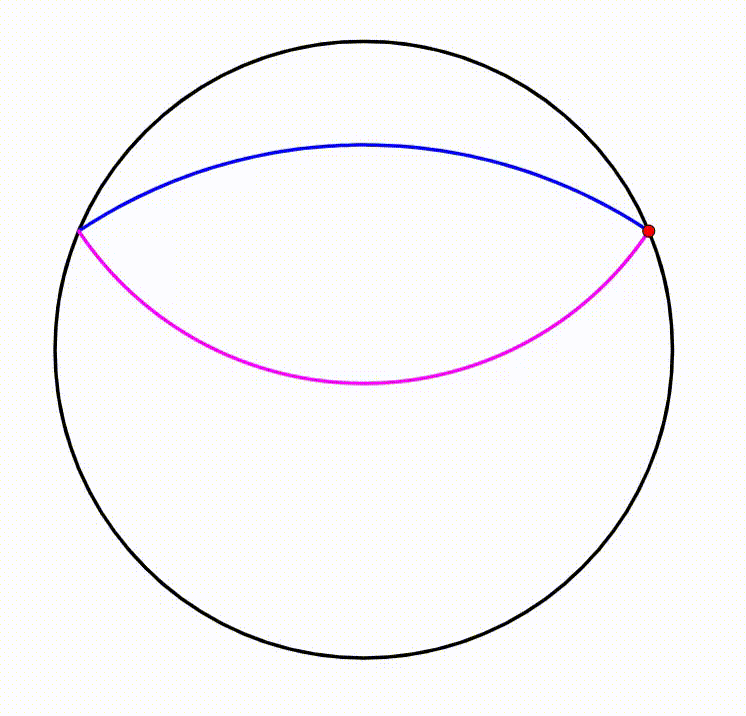 The diagram shows a black circle. A horizontal yellow chord is drawn creating two circular segments, their respective heights are
and
. The red point moves freely along the black circle. We use this chord and the red point to draw the yellow triangle. The triangle's incenter (green point) traces a
locus
(purple curve and blue curve). The area bounded by both curves can be expressed as:
The diagram shows a black circle. A horizontal yellow chord is drawn creating two circular segments, their respective heights are
and
. The red point moves freely along the black circle. We use this chord and the red point to draw the yellow triangle. The triangle's incenter (green point) traces a
locus
(purple curve and blue curve). The area bounded by both curves can be expressed as:
where , , , and are positive integers. and are coprime. Find .
The answer is 252.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the center of the circle be O , the triangle A B C , where A B is the horizontal chord, the center and radius of the incircle at any moment be P and r , and P N and O M be perpendicular to A B . Since the heights of two circular segments are 4 and 9 , the diameter of the circle is 1 3 , hence its radius 6 . 5 . Then A M = B M = 6 and O M = 2 . 5 . The smaller ∠ A O B = 2 tan − 1 5 1 2 and the larger ∠ A O B = 2 π − 2 tan − 1 5 1 2 . When C is on top, ∠ A C B = 2 1 ( 2 π − 2 tan − 1 5 1 2 ) = π − tan − 1 5 1 2 . Let ∠ C A B = θ , then ∠ C B A = tan − 1 5 1 2 − θ , and
A N + N B r cot 2 θ + r cot ( 2 1 tan − 1 5 1 2 − 2 θ ) t r + 3 2 − t 1 + 3 2 t ⋅ r ⟹ r = A B = 1 2 = 1 2 = t 1 + 2 − 3 t 3 + 2 t 1 2 = 1 + t 2 6 t ( 2 − 3 t ) Let t = tan 2 θ
Let the midpoint of A B be the origin of the x y -plane and an arbitrary point on the upper locus be P ( x , y ) . Then
⎩ ⎪ ⎨ ⎪ ⎧ y = r = 1 + t 2 6 t ( 2 − 3 t ) x = t r − 6 = 1 + t 2 6 ( 2 − 3 t ) − 6
Then the area under the locus is
A 1 = ∫ − 6 6 y d x = ∫ − 6 6 1 + t 2 6 t ( 2 − 3 t ) d ( 1 + t 2 6 ( 2 − 3 t ) − 6 ) = ∫ 0 3 2 ( 1 + t 2 ) 3 3 6 t ( 2 − 3 t ) ( 3 + 4 t − 3 t 2 ) d t = 1 1 7 tan − 1 3 2 − 5 4
Similarly, when C is at the bottom, ∠ A C B is half the smaller ∠ A O B , ⟹ ∠ A C B = tan − 1 5 1 2 , r = y = 1 + t 2 4 t ( 3 − 2 t ) , x = 1 + t 2 4 ( 3 − 2 t ) − 6 , and the area under the locus is
A 2 = ∫ − 6 6 y d x = ∫ − 6 6 1 + t 2 4 t ( 3 − 2 t ) d ( 1 + t 2 4 ( 3 − 2 t ) − 6 ) = ∫ 0 2 3 ( 1 + t 2 ) 3 3 6 t ( 2 − 3 t ) ( 3 + 4 t − 3 t 2 ) d t = 5 2 tan − 1 2 3 − 2 4
Therefore A 1 + A 2 = 1 1 7 tan − 1 3 2 + 5 2 tan − 1 2 3 − 7 8 and p + q + m + n + 1 = 1 1 7 + 5 2 + 2 + 3 + 7 8 = 2 5 2