Dynamic Geometry: P109

The radius of the circle is $R=\dfrac{4+9}{2}=6.5$ . We place the configuration on a coordinate system, so that the center of the circle is the origin and the common cord $AB$ of the circular segments lies on the line $y=2.5$ , as seen on the figure. Due to symmetry, $A$ and $B$ have opposite $x$ -coordinates. Their $y$ -coordinate is $2.5$ . The equation of the circle is ${{x}^{2}}+{{y}^{2}}={{\left( 6.5 \right)}^{2}}$ We focus on the upper circular segment. Let $C\left( {{x}_{1}},{{y}_{1}} \right)$ be the third vertex of the cyan triangle. The largest rectangle inscribed in $ABC$ with its base on $AB$ is the one that joints the midpoints $M$ , $N$ of $CA$ and $CB$ respectively. Let $P$ , $Q$ be the other two vertices of the rectangle. The center $E$ of $MNPQ$ is the midpoint of $MP$ , so we have ${{x}_{E}}=\dfrac{{{x}_{M}}+{{x}_{P}}}{2}=\dfrac{\dfrac{{{x}_{A}}+{{x}_{C}}}{2}+{{x}_{N}}}{2}=\dfrac{\dfrac{{{x}_{A}}+{{x}_{1}}}{2}+\dfrac{{{x}_{C}}+{{x}_{B}}}{2}}{2}=\dfrac{\cancel{{{x}_{A}}}+2{{x}_{1}}+\cancel{{{x}_{B}}}}{4}=\dfrac{{{x}_{1}}}{2}$ $\Rightarrow {{x}_{1}}=2{{x}_{E}}$ ${{y}_{E}}=\dfrac{{{y}_{M}}+{{y}_{P}}}{2}=\dfrac{\dfrac{{{y}_{A}}+{{y}_{C}}}{2}+{{y}_{A}}}{2}=\dfrac{3{{y}_{A}}+{{y}_{1}}}{4}=\dfrac{3\times 2.5+{{y}_{1}}}{4}=\dfrac{2{{y}_{1}}-15}{8}$ $\Rightarrow {{y}_{1}}=\dfrac{8{{y}_{E}}-15}{2}$ Since $C$ belongs to the circle, it holds $\begin{aligned} {{x}_{1}}^{2}+{{y}_{1}}^{2}={{\left( 6.5 \right)}^{2}} & \Rightarrow {{\left( \dfrac{{{x}_{E}}}{2} \right)}^{2}}+{{\left( \dfrac{8{{y}_{E}}-15}{2} \right)}^{2}}={{\left( 6.5 \right)}^{2}} \\ & \Rightarrow \dfrac{{{x}_{E}}^{2}}{{{\left( \dfrac{13}{4} \right)}^{2}}}+\dfrac{{{\left( {{y}_{E}}-\dfrac{15}{8} \right)}^{2}}}{{{\left( \dfrac{13}{8} \right)}^{2}}}=1 \\ \end{aligned}$ Hence, the center $E$ of the red rectangle $MNPQ$ belongs to the ellipse with equation $\dfrac{{{x}^{2}}}{{{\left( \dfrac{13}{4} \right)}^{2}}}+\dfrac{{{\left( y-\dfrac{15}{8} \right)}^{2}}}{{{\left( \dfrac{13}{8} \right)}^{2}}}=1$ In fact it traces the part of the ellipse that is over the cord $AB$ $\left( y\ge 2.5 \right)$ .

Working likewise, we find that the center of the green rectangle traces the rest of the same ellipse.

The semi-axes of the ellipse are $a=\dfrac{13}{4}$ and $b=\dfrac{13}{8}$ , thus the area of the locus is $A=ab\pi =\frac{13}{4}\cdot \dfrac{13}{8}\cdot \pi =\dfrac{169}{32}\pi$ For the answer, $p=169$ , $q=32$ , thus, $p+q=\boxed{201}$ .

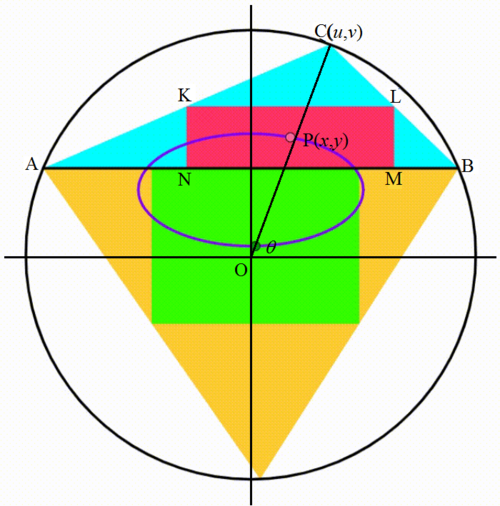
$\red{[\text{Updated to provide a shorter explanation.}]}$ . Let $O$ , the center of the circle, be the origin $(0,0)$ of the $xy$ -plane, the variable triangle be $\triangle ABC$ (note that $\triangle ABC$ follows the same equations whether $C$ is on top or at the bottom), $OC$ makes an angle of $\theta$ with the $x$ -axis. Referring to the calculations in Dynamic Geometry: P96 Series , the circle has a radius of $6.5$ , $AB = 12$ , $AB$ is along $y=2.5$ , and the largest rectangle inscribed by a triangle has a height and breadth half of those of the triangle.

Then $C=(u,v) = (6.5 \cos \theta, 6.5 \sin \theta)$ . The height of $KLMN$ , $NK=LM = \dfrac {v - 2.5} 2 = \dfrac {6.5 \sin \theta - 2.5}2$ . Note that $\triangle KLC$ and $\triangle ABC$ are similar, then $KL = \dfrac {AB}2 = 6$ , the $x$ -coordinate of $K$ and $N$ , $x_K = \dfrac {6.5 \cos \theta - 6}2$ and that of $L$ and $M$ , $x_L = \dfrac {6.5 \cos \theta + 6}2$ . Let the arbitrary point on the locus or the center of rectangle $KLMN$ be $P(x,y)$ . Then the coordinates of $P$ :

$\begin{cases} x = \dfrac {x_K+x_L}2 = \dfrac {13 \cos \theta}4 & \implies \dfrac {4x}{13} = \cos \theta \\ y = \dfrac {LM+2.5+2.5}2 = \dfrac {13 \sin \theta}8 + \dfrac 3{16} & \implies \dfrac 8{13} \left(y - \dfrac 3{16} \right) = \sin \theta \end{cases} \\ \implies \frac {x^2}{\left(\frac {13}4\right)^2} + \frac {\left(y-\frac 3{16}\right)^2}{\left(\frac {13}8\right)^2} = 1$

Therefore the locus is an ellipse with center at $\left(0, \dfrac 3{16}\right)$ , a major semi-axis $a = \dfrac {13}4$ , a minor semi-axis $b = \dfrac {13}8$ , and an area of $ab \pi = \dfrac {13}4 \cdot \dfrac {13}8 \pi = \dfrac {169}{32} \pi$ . $\implies p + q = 169+32 = \boxed{201}$ .