Dynamic Geometry: P110
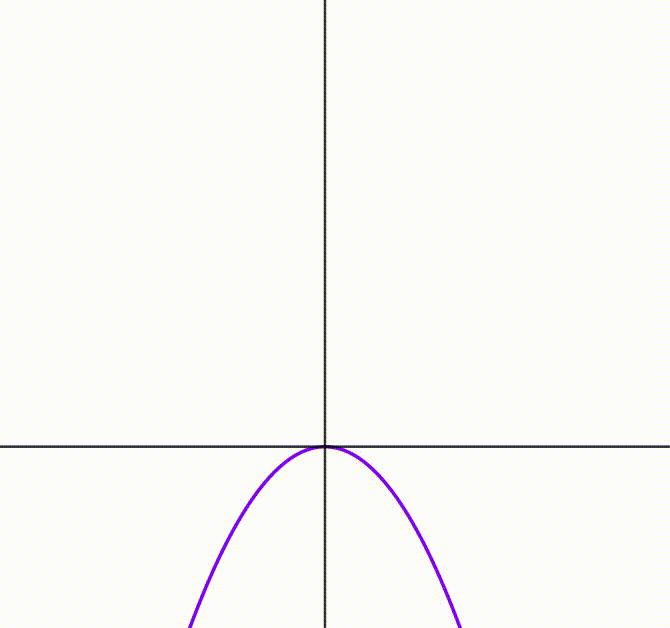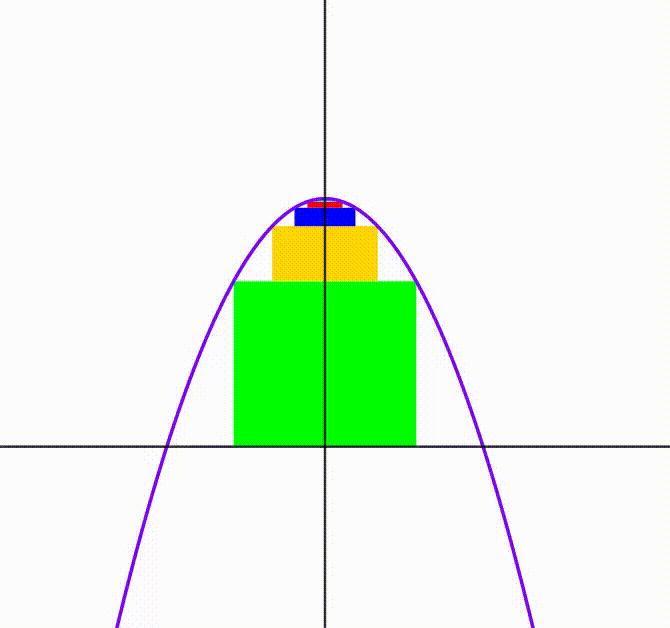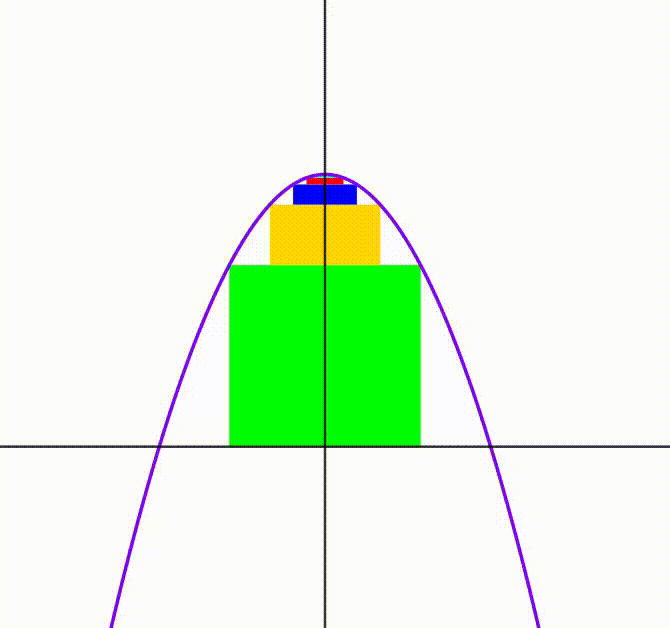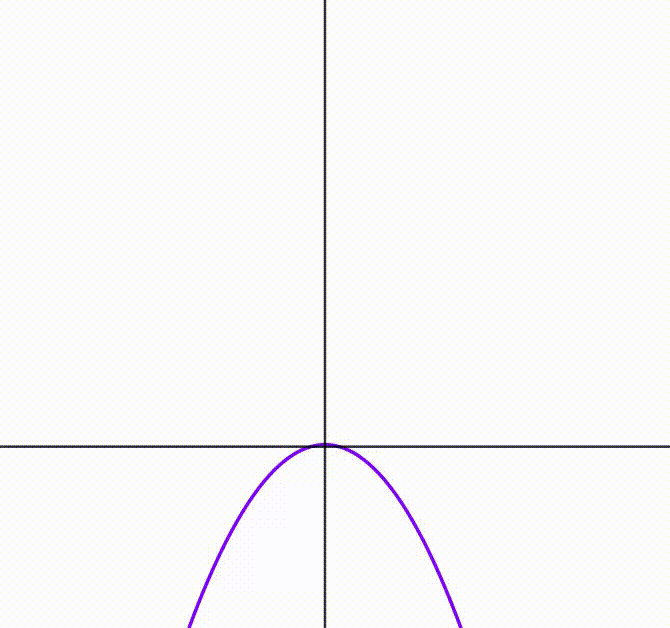 The diagram shows a parabola
. We translate the function vertically to the top and move it back to its normal position freely. An infinite number of rectangles is inscribed between the parabola and the
axis and placed on the top of each other. The rectangles are drawn so their area is always the
maximum
possible. When the perimeter of the
rectangle is equal to
, the sum of the heights of all rectangle converges to
, where
and
are coprime positive integers. Find
.
The diagram shows a parabola
. We translate the function vertically to the top and move it back to its normal position freely. An infinite number of rectangles is inscribed between the parabola and the
axis and placed on the top of each other. The rectangles are drawn so their area is always the
maximum
possible. When the perimeter of the
rectangle is equal to
, the sum of the heights of all rectangle converges to
, where
and
are coprime positive integers. Find
.
- Note : Heights are each rectangle's both vertical segments
The answer is 59051.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We can define the variable parabola as y = h − x 2 , where h ≥ 0 is the variable height of the parabola O V . Define the right top vertex of n th rectangle be ( x n , y n ) and its height h n , then h n = y n − y n − 1 , y n = ∑ k = 1 n h k , and y n = h − x n 2 .
Now let us consider the largest rectangle inscribed by y = h − x 2 . The area of the rectangle is given by:
A d x d A ⟹ x 1 y 1 = 2 x y = 2 x ( h − x 2 ) = 2 h − 6 x 2 = 3 h = h − 3 h = 3 2 h = h 1 To find the maximum area Putting d x d A = 0
As the pattern repeats,
h 2 h 3 h 4 ⟹ h n y n ⟹ x n = 3 2 ( h − h 1 ) = 9 2 h = 3 2 ( h − h 1 − h 2 ) = h 2 − 3 2 h 2 = 3 h 2 = 3 2 2 h = 3 h 3 = 3 4 2 h = 3 n 2 h = k = 1 ∑ n h k = k = 1 ∑ n 3 k 2 h = h − 3 n h = h − x n 2 = 3 n h
Given that the perimeter of the 1 6 th rectangle is 7 2 9 5 5 ,
4 x n + 2 y n 3 8 4 h + 3 1 6 4 h 3 1 6 h + 3 8 h ( 3 8 h + 2 1 ) 2 3 8 h h ⟹ h = 7 2 9 5 5 = 7 2 9 5 5 = 2 9 1 6 5 5 = 2 9 1 6 5 5 + 4 1 = 2 7 1 4 − 2 1 = 5 4 1 = 2 3 5 = 4 5 9 0 4 9
The sum of pairs of heights of the rectangles
n = 1 ∑ ∞ 2 h n = n = 1 ∑ ∞ 3 2 4 h = 3 4 h ⋅ 1 − 3 1 1 = 2 h = 2 5 9 0 4 9
Therefore p + q = 5 9 0 4 9 + 2 = 5 9 0 5 1 .