Dynamic Geometry: P111
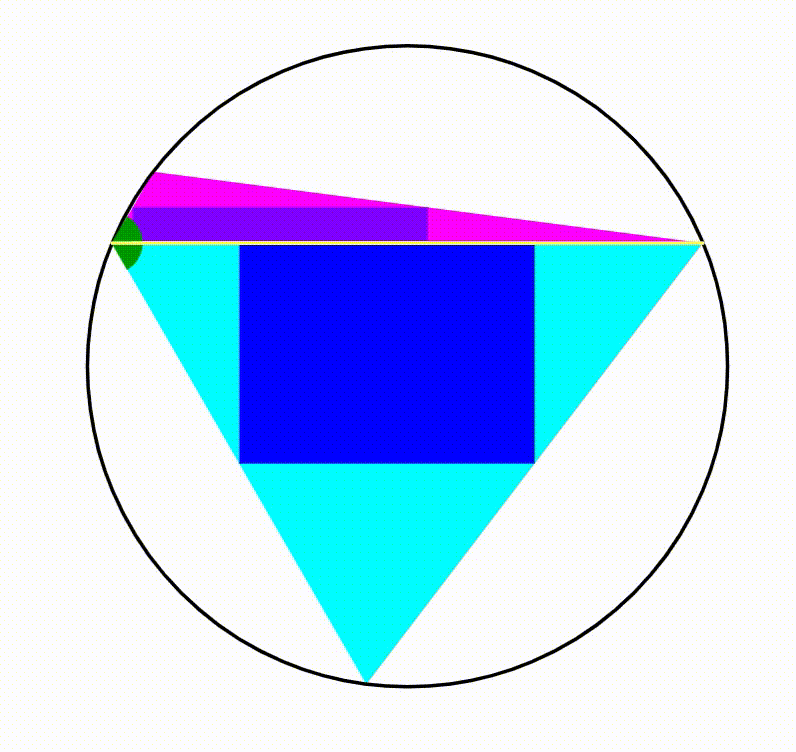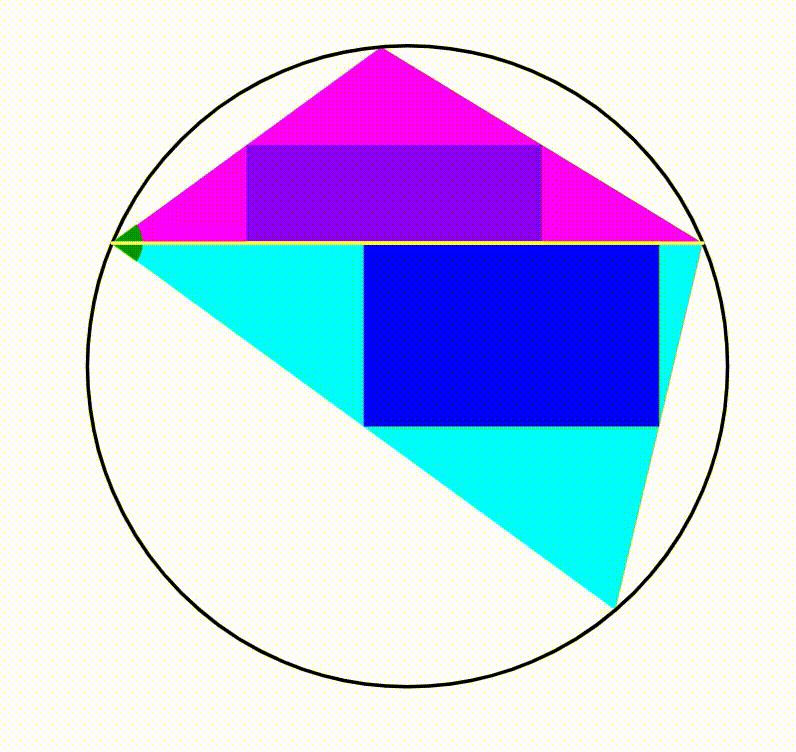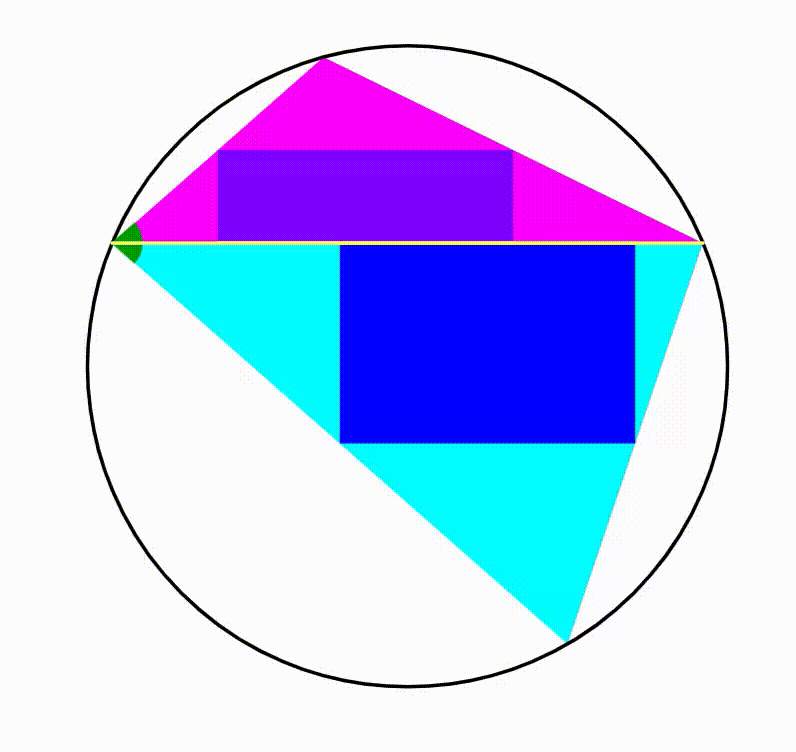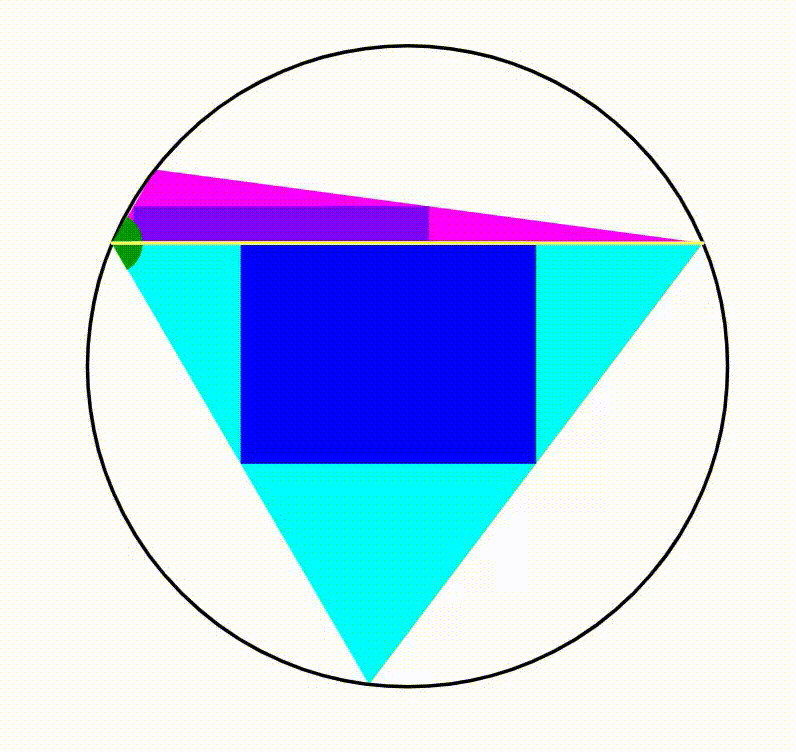 The diagram shows a black circle. A horizontal yellow chord is drawn creating two circular segments, their respective heights are
4
and
9
. In each circular segment, we inscribe a triangle. In both triangles we inscribe the largest rectangle possible. The triangles are both evolving so that the two green angles are always equal. When the ratio of upper rectangle's area to the lower rectangle's area is equal to
6
1
1
1
, the distance between the two moving points of both triangles can be expressed as
q
p
, where
p
and
q
are coprime positive integers. Find
p
+
q
.
The diagram shows a black circle. A horizontal yellow chord is drawn creating two circular segments, their respective heights are
4
and
9
. In each circular segment, we inscribe a triangle. In both triangles we inscribe the largest rectangle possible. The triangles are both evolving so that the two green angles are always equal. When the ratio of upper rectangle's area to the lower rectangle's area is equal to
6
1
1
1
, the distance between the two moving points of both triangles can be expressed as
q
p
, where
p
and
q
are coprime positive integers. Find
p
+
q
.
The answer is 212.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Great use of the intersecting chord theorem!
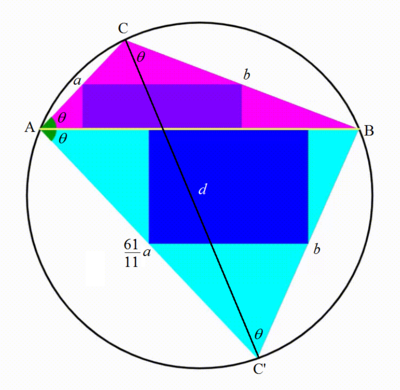
[Updated to provide a better explanation.] Let the dividing chord of the circle be A B , the upper and lower variable triangles be △ A B C and △ A B C ′ respectively, and the measure of the green angle be θ . Referring the calculations in Dynamic Geometry: P96 Series , the radius of the circle is 6 . 5 , A B = 1 2 , ∠ A C B = π − tan − 1 5 1 2 , ∠ A C ′ B = tan − 1 5 1 2 , and the biggest rectangle inscribed by a triangle is one with half the height and width of those of the triangle.
[Updated; much simpler solution using cyclic quadrilateral.] Since △ A B C and △ A B C ′ have the same base A B = 1 2 , the width of both upper and lower rectangles is 6 . The heights of the two triangles are h = A C sin θ and h ′ = A C ′ sin θ . Then the ratio of their areas ' 6 ⋅ 2 h ′ 6 ⋅ 2 h = 6 ⋅ 2 1 A C ′ sin θ 6 ⋅ 2 1 A C sin θ = A C ′ A C = 6 1 1 1
If A C = a , A C ′ = 1 1 6 1 a = k a , where k = 1 1 6 1 .
Since A C B C ′ is a cyclic quadrilateral , ∠ B C C ′ = ∠ B A C ′ = θ and ∠ B C ′ C = ∠ B A C = θ . Therefore △ B C C ′ is isosceles and B C = B C ′ = b . By cosine rule ,
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ a 2 + b 2 − 2 a b cos ( π − tan − 1 5 1 2 ) = a 2 + b 2 + 1 3 1 0 a b = 1 4 4 k 2 a 2 + b 2 − 2 k a b cos ( tan − 1 5 1 2 ) = k 2 a 2 + b 2 − 1 3 1 0 k a b = 1 4 4 . . . ( 1 ) . . . ( 2 ) ( 2 ) − ( 1 ) : ( k 2 − 1 ) a 2 − 1 3 1 0 a b ( k + 1 ) ⟹ b ( 1 ) : a 2 + 1 1 2 6 5 2 a 2 + 1 3 1 0 ⋅ 1 1 6 5 a 2 ⟹ a b = 0 = 1 0 1 3 a ( k − 1 ) = 1 0 1 3 a ( 1 1 6 1 − 1 ) = 1 1 6 5 a = 1 4 4 = 3 4 1 1 = 3 4 6 5
Let the distance between the two moving points C C ′ = d . By Ptolemy's theorem ,
A B ⋅ C C ′ 1 2 d ⟹ d = A C ⋅ B C ′ + A C ′ ⋅ B C = a b + 1 1 6 1 a b = 1 1 7 2 a b = 1 1 7 2 ⋅ 3 4 1 1 ⋅ 6 5 = 1 7 1 9 5
Therefore p + q = 1 9 5 + 1 7 = 2 1 2 .
Thank you for posting.
Log in to reply
Updated my solution/ Much easier using cyclic quadrilateral.
Log in to reply
Well done, I did not even thought about using cyclic quadrilateral.
By Intersecting Cords Theorem ,
A M ⋅ M B = E M ⋅ M F ⇒ ( 2 A B ) 2 = 4 × 9 ⇒ A B = 1 2 We place the configuration on a coordinate system, so that the center of the circle is point K ( 0 , − 2 . 5 ) . Then, the equation of the circle is x 2 + ( y + 2 . 5 ) 2 = 6 . 5 2 The common cord A B of the circular segments lies on the x -axis with A ( − 6 , 0 ) and B ( 6 , 0 ) . Let the upper triangle be △ C A B and the lower △ D A B , as seen on the figure. Since the biggest rectangle inscribed in each triangle has half the height and half the width of the corresponding triangle, its area is one fourth the area of the triangle.
Consequently, denoting each green angle by θ , we have 6 1 1 1 = area of lower rectangle area of upper rectangle = 2 1 [ C D B ] 2 1 [ C A B ] = 2 1 A B ⋅ A D ⋅ sin θ 2 1 A B ⋅ A C ⋅ sin θ = A D A C ⇒ A D = 1 1 6 1 A C ( 1 ) Because the green angles are equal, the reflection C ′ of point C w.r.t. the x -axis lies on A D , thus, vectors A C ′ and A D have the same direction.
Using points A ( − 6 , 0 ) , hence, taking into account ( 1 ) and the fact that A C ′ = A C , we have
A D = 1 1 6 1 A C ′ 0 ⇒ ( x D − x A , y D − y A ) = 1 1 6 1 ( x C ′ − x A , y C ′ − y A ) ⇒ ( x D + 6 , y D ) = 1 1 6 1 ( x C + 6 , − y C ) ⇒ ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ x D = 1 1 6 1 x C + 3 0 0 0 y D = − 1 1 6 1 y C ( 2 ) Since both points C and D belong to the circle we get the system of equations
⎩ ⎨ ⎧ x C 2 + ( y C + 2 . 5 ) 2 = 6 . 5 2 0 x D 2 + ( y D + 2 . 5 ) 2 = 6 . 5 2 ⇔ ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ x C 2 + ( y C + 2 . 5 ) 2 = 6 . 5 2 0 ( 1 1 6 1 x C + 3 0 0 ) 2 + ( − 1 1 6 1 y C ) 2 = 6 . 5 2 which solves to x C = − 3 4 1 7 1 y C = 3 4 5 5 Consequently,
( 2 ) ⇒ ( x D , y D ) = ( − 3 4 2 1 , − 3 4 3 0 5 ) Now we can calculate the length of C D :
C D = ( x D − x C ) 2 + ( y D − y C ) 2 = ( − 3 4 2 1 + 3 4 1 7 1 ) 2 + ( − 3 4 3 0 5 − 3 4 5 5 ) 2 = 1 7 1 9 5 For the answer, p = 1 9 5 , q = 1 7 , thus, p + q = 2 1 2 .