Dynamic Geometry: P133
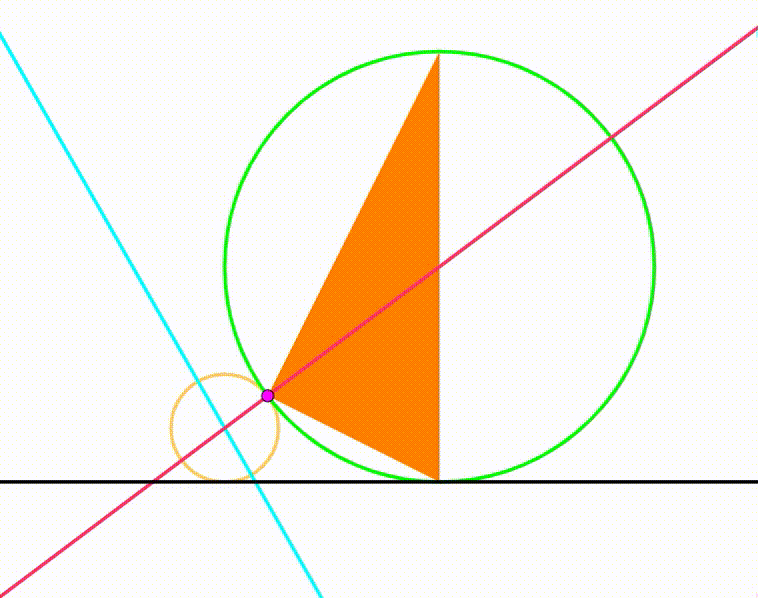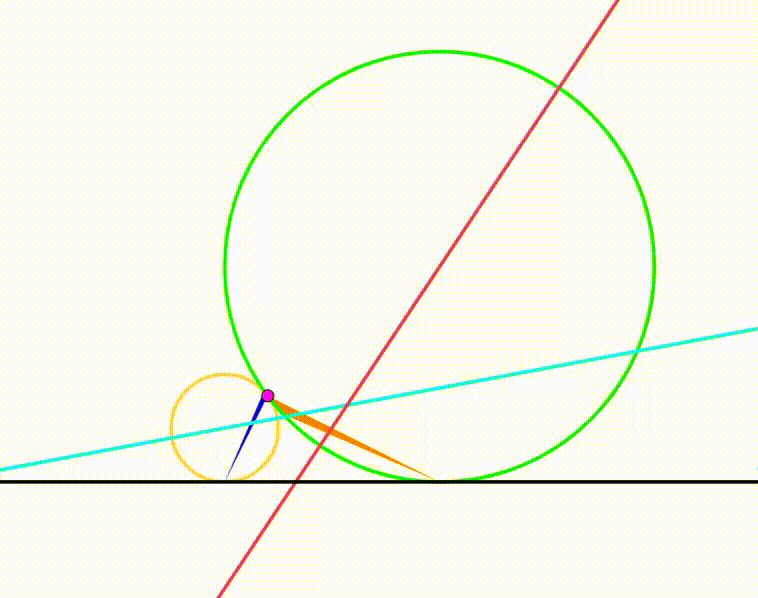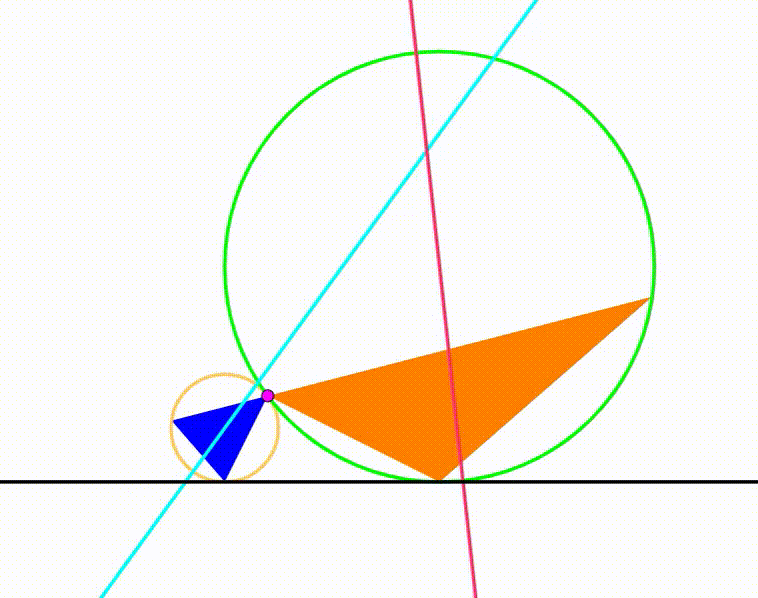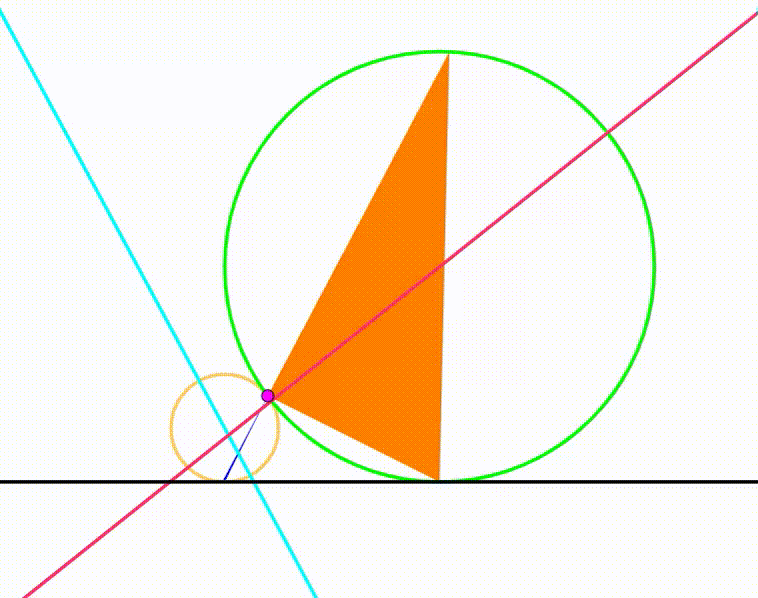 The diagram shows a yellow circle with radius
and a green circle with radius
. They are tangent to each other and tangent to the same black horizontal line. The purple point is their tangency point. The cyan line passes through this point and rotates freely so that we can draw two triangles (blue and orange) using the purple tangency point, the tangency point between the circles and the black horizontal line and the intersection points between the cyan line and both circles. The cyan and red lines are the the Eurler lines. When the Euler lines are perpendicular, the ratio of the blue triangle's area to the area of the orange triangle can be expressed as:
The diagram shows a yellow circle with radius
and a green circle with radius
. They are tangent to each other and tangent to the same black horizontal line. The purple point is their tangency point. The cyan line passes through this point and rotates freely so that we can draw two triangles (blue and orange) using the purple tangency point, the tangency point between the circles and the black horizontal line and the intersection points between the cyan line and both circles. The cyan and red lines are the the Eurler lines. When the Euler lines are perpendicular, the ratio of the blue triangle's area to the area of the orange triangle can be expressed as:
where , , , and are positive integers. and are coprime, so are and . is square-free. Find .
Note : There are two situations where the Euler lines are perpendicular, we focuse on the case where the sum of the areas of the triangles is minimum.
The answer is 108.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the tangent point of the two circles be O ( 0 , 0 ) , the origin of the x y -plane, the center of the circle with radius 1 be O 1 ( − 1 , 0 ) , the center of the circle with radius 4 be O 2 ( 4 , 0 ) , A B be the moving line through O with a gradient of tan θ , C and D be the vertices on the black line of the blue and orange triangles respectively. Then the points are
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ A = ( − cos 2 θ − 1 , − sin 2 θ ) B = ( 4 cos 2 θ + 4 , 4 sin 2 θ ) C = ( − 5 8 , − 5 4 ) D = ( 5 8 , − 5 1 6 )
Then the centroids P and Q of △ A C O and △ B D O are:
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ P = ( − 1 5 5 cos 2 θ + 1 3 , − 1 5 5 sin 2 θ + 4 ) Q = ( 1 5 2 0 cos 2 θ + 2 8 , 1 5 2 0 sin 2 θ − 1 6 )
Since Euler line passes through the centroid and circumcenter of the triangle, the two Euler lines are:
⎩ ⎪ ⎨ ⎪ ⎧ O 1 P : O 2 Q : x + 1 y = 5 cos 2 θ − 2 5 sin 2 θ + 4 x − 4 y = 5 cos 2 θ − 8 5 sin 2 θ − 4
Note that the right-hand side of the two equations above are the gradients of the respective Euler lines. When the two Euler lines are perpendicular, we have:
5 cos 2 θ − 2 5 sin 2 θ + 4 ⋅ 5 cos 2 θ − 8 5 sin 2 θ − 4 ( 5 sin 2 θ + 4 ) ( 5 sin 2 θ − 4 ) 2 5 sin 2 2 θ − 1 6 5 0 cos 2 θ cos 2 θ ⟹ θ = − 1 = − ( 5 cos 2 θ − 2 ) ( 5 cos 2 θ − 8 ) = − 2 5 cos 2 2 θ + 5 0 cos 2 θ − 1 6 = 2 5 = 2 1 = ± 3 0 ∘
The sum of areas of the two triangles is smaller when θ = 3 0 ∘ . By shoelace formula , the areas of the two triangles are:
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ A 1 = 2 1 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 0 0 1 − cos ( − 6 0 ∘ ) − 1 − sin ( − 6 0 ∘ ) 1 − 5 8 − 5 4 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ = 5 3 + 2 3 A 2 = 2 1 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 0 0 1 4 cos ( − 6 0 ∘ ) + 4 4 sin ( − 6 0 ∘ ) 1 5 8 − 5 1 6 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ = 5 8 ( 6 − 3 )
⟹ A 2 A 1 = 8 ( 6 − 3 ) 3 + 2 3 = 1 1 1 + 8 8 5 3
Therefore p + q + l + m + n = 1 + 1 1 + 5 + 3 + 8 8 = 1 0 8 .