Dynamic Geometry: P18
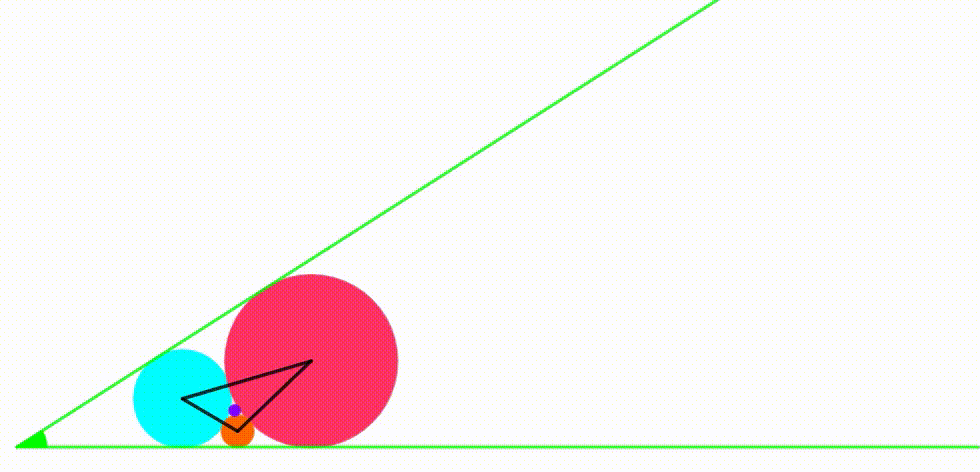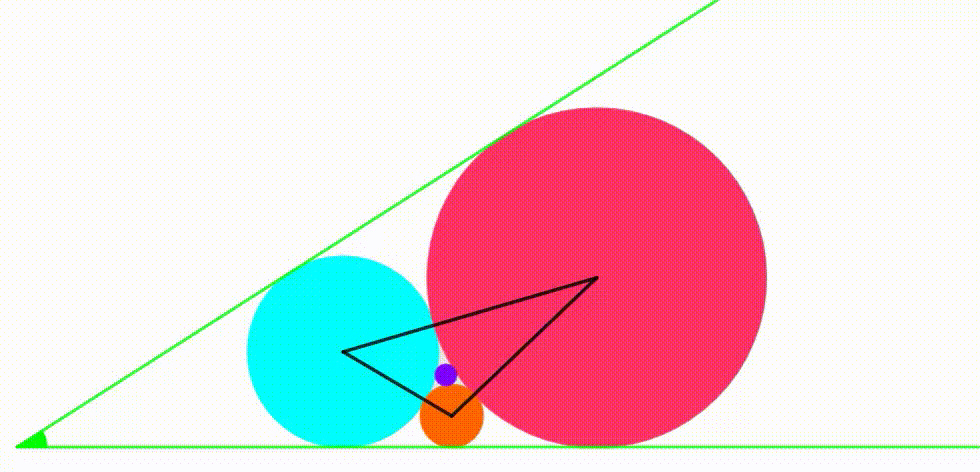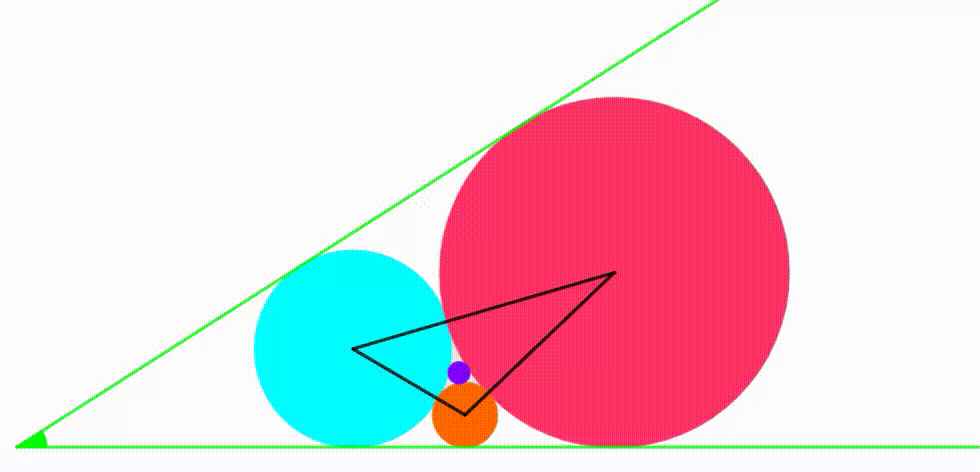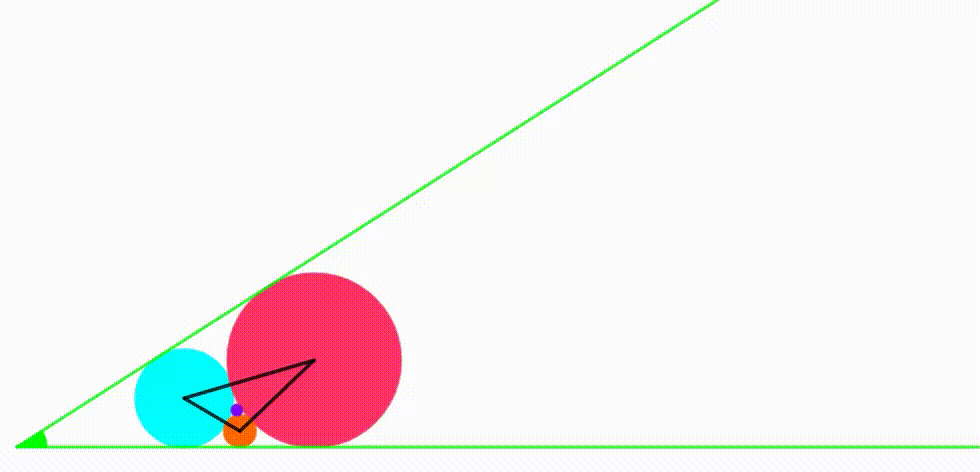 The diagram shows a green angle which tangent is equal to
5
2
7
3
3
6
. Three circles (orange, cyan and red) tangent to each other and internally tangent to the angle are moving freely inside the angle. Using each center, a black triangle is drawn. A fourth purple circle is drawn so it's tangent to the three inital circles. When the area of the black triangle is equal to
1
6
3
7
, the radius of the purple circle can be expressed as
b
a
, where
a
and
b
are coprime positive integers. Find
a
+
b
.
The diagram shows a green angle which tangent is equal to
5
2
7
3
3
6
. Three circles (orange, cyan and red) tangent to each other and internally tangent to the angle are moving freely inside the angle. Using each center, a black triangle is drawn. A fourth purple circle is drawn so it's tangent to the three inital circles. When the area of the black triangle is equal to
1
6
3
7
, the radius of the purple circle can be expressed as
b
a
, where
a
and
b
are coprime positive integers. Find
a
+
b
.
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Hello there ! Thank you for posting !
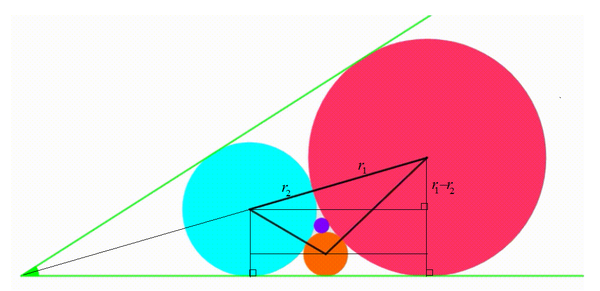
Let the radius of the red, cyan, orange, and purple circles be r 1 , r 2 , r 3 , and r 4 respectively. Let the green angle to be θ , then we note that the line joining the centers of the red and cyan circles has a gradient of tan 2 θ . SInce tan θ = 5 2 7 3 3 6 , then tan 2 θ = sin θ 1 − cos θ = 2 4 7 ⟹ sin 2 θ = 2 5 7 and
r 1 + r 2 r 1 − r 2 = sin 2 θ = 2 5 7 ⟹ r 2 = 1 6 9 r 1
We note that the horizontal distance between the centers of the red can cyan circles is given by ( r 1 + r 2 ) 2 − ( r 1 − r 2 ) 2 = 2 r 1 r 2 . This formula is applicable to any two circles. So we have:
2 r 2 r 3 + 2 r 3 r 1 = 2 r 1 r 2 ⟹ r 3 = r 1 + r 2 r 1 r 2 = 7 3 r 1 ⟹ r 3 = 4 9 9 r 1
Then the three sides of the triangle is r 1 + r 2 , r 2 + r 3 , and r 3 + r 1 . By Heron's formula , the area of the triangle is
: ( r 1 + r 2 + r 3 ) r 1 r 2 r 3 = 7 8 4 3 3 3 r 1 2 = 1 6 3 7 ⟹ r 1 = 3 7
Then r 2 = 1 6 9 r 1 = 1 6 2 1 and r 3 = 4 9 9 r 1 = 7 3 . Thanks to @David Vreken and of course Descartes' theorem , with three know radii we can find the radius of the fourth circle which is tangent to the other three circles as follows:
r 4 1 ⟹ r 4 = r 1 1 + r 2 1 + r 3 1 + 2 r 1 1 r 2 1 + r 2 1 r 3 1 + r 3 1 r 1 1 = 2 1 1 4 8 = 1 4 8 2 1
Therefore a + b = 2 1 + 1 4 8 = 1 6 9 = 1 3
Thank you for posting !
@Valentin Duringer , I was actually referring to " When the area of the black triangle is equal to..." Use "when" instead of "if". Because the triangle is moving to and forth and the area changes, therefore it is when (as you put it at the precise moment) the circle is having an area and not if
Ok,"when" = moment, "if" = never changing data
Label the diagram as follows, and let p , q , r , t be the radii of the cyan, orange, red, and purple circles, respectively, and let θ = ∠ O A E :
Since the centers of the cyan and red circles lie on the bisector of the green angle, tan 2 θ = 5 2 7 3 3 6 = 1 − tan 2 θ 2 tan θ , which solves to tan θ = 2 4 7 .
Then from △ O A E and △ O B D , O A = 7 2 4 p and O B = 7 2 4 r .
Since E D = r + p and D C = r − p , by the Pythagorean Theorem on △ E D C we have E C = ( r + p ) 2 − ( r − p ) 2 = 2 p r = A B .
Since O A + A B = O B , 7 2 4 p + 2 p r = 7 2 4 r , which rearranges to r = 9 1 6 p .
By Descartes' Theorem on the cyan, orange, and red circles and the line, q 1 = p 1 + r 1 + 2 p r 1 = p 1 + 1 6 p 9 + 2 1 6 p 2 9 = 1 6 p 4 9 , which solves to q = 4 9 1 6 p .
The semiperimeter s of the black triangle is then p + q + r , and s − a , s − b , and s − c are p , q , and r , so that by Heron's formula the area of the triangle is T = s ( s − a ) ( s − b ) ( s − c ) = ( p + q + r ) p q r = ( p + 4 9 1 6 p + 9 1 6 p ) ⋅ p ⋅ 4 9 1 6 p ⋅ 9 1 6 p = 4 4 1 5 9 2 p 2 = 1 6 3 7 , which solves to p = 1 6 2 1 .
That means q = 4 9 1 6 p = 4 9 1 6 ⋅ 1 6 2 1 = 4 9 2 1 and r = 9 1 6 p = 9 1 6 ⋅ 1 6 2 1 = 3 7 .
Finally, by Descartes' Theorem on all four circles, t 1 = 2 1 1 6 + 2 1 4 9 + 7 3 + 2 2 1 1 6 ⋅ 2 1 4 9 + 2 1 1 6 ⋅ 7 3 + 2 1 4 9 ⋅ 7 3 = 2 1 1 4 8 , which solves to t = 1 4 8 2 1 .
Therefore, a = 2 1 , b = 1 4 8 , and a + b = 1 3 .