Dynamic Geometry: P19
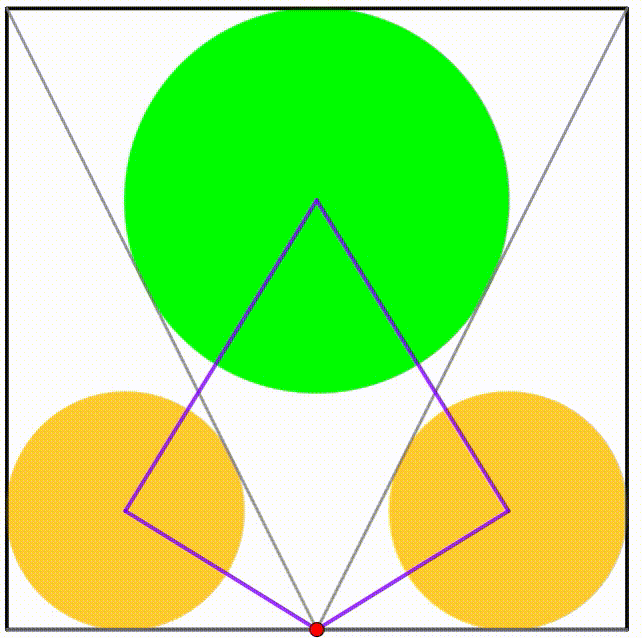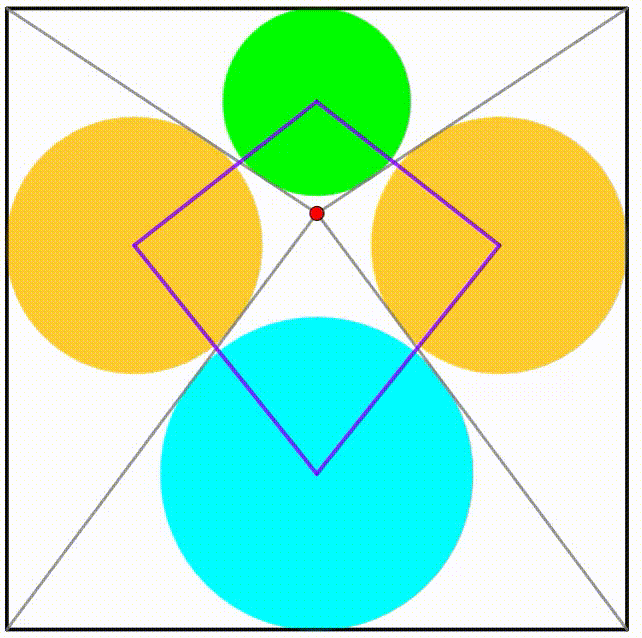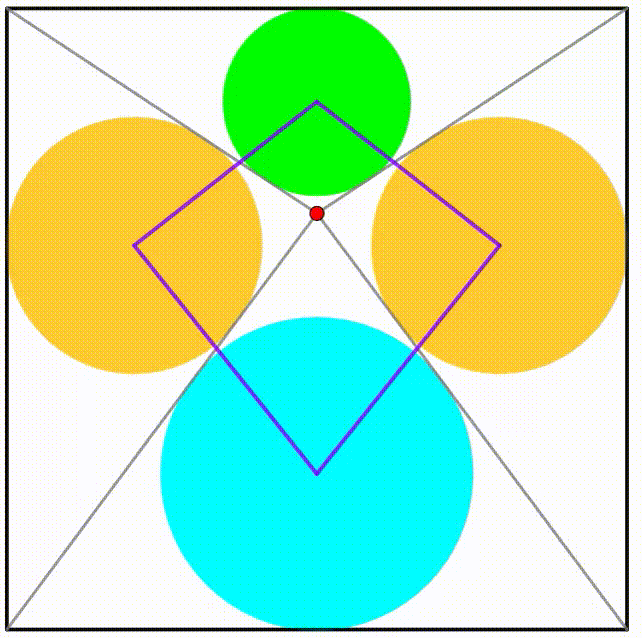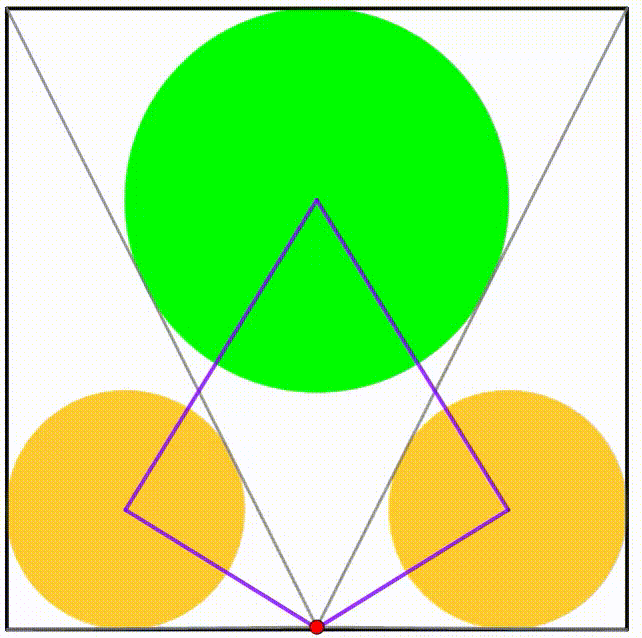 The diagram shows a unit black square. A red point is freely moving along the square's vertical symmetry axis. Four triangles can be drawn with their incircle. Using each circle's center we can draw a purple quadrilateral. If the area of the quadrilateral is equal to
, the radius of the smallest circle can be expressed as
, where
and
are coprime positive integers. Find
.
The diagram shows a unit black square. A red point is freely moving along the square's vertical symmetry axis. Four triangles can be drawn with their incircle. Using each circle's center we can draw a purple quadrilateral. If the area of the quadrilateral is equal to
, the radius of the smallest circle can be expressed as
, where
and
are coprime positive integers. Find
.
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the radii of the cyan, green, and orange circle be r 1 , r 2 , and r 3 respectively, and the height of the red point to the base of the square be h . From the equation A = s r , where A , s , and r are the area, semiperimeter, and the inradius of a triangle. Then we have:
r 1 r 2 r 3 = 2 h 2 + 4 1 + 1 h = 4 h 2 + 1 + 1 h = 4 ( 1 − h ) 2 + 1 − 1 1 − h = 4 h 2 + 1 + 4 ( 1 − h ) 2 + 1 + 2 1 Replace h with 1 − h .
We note that the area of the purple quadrilateral is half of the red rectangle shown. Therefore we need to find the h , when
2 ( 1 − r 1 − r 2 ) ( 1 − 2 r 3 ) = 2 4 0 7 4 1 − 3
Solving the equation above, we get h = 8 5 . Then r 1 = 1 6 4 + 8 5 ≈ 0 . 2 4 0 3 1 2 4 2 4 , r 2 = 6 1 ≈ 0 . 1 6 6 6 6 6 6 6 7 , and r 3 = 4 1 + 1 3 4 ≈ 0 . 2 0 6 1 5 2 3 6 8 . Therefore r 2 = 6 1 is the smallest and a + b = 7 .