Dynamic Geometry: P20
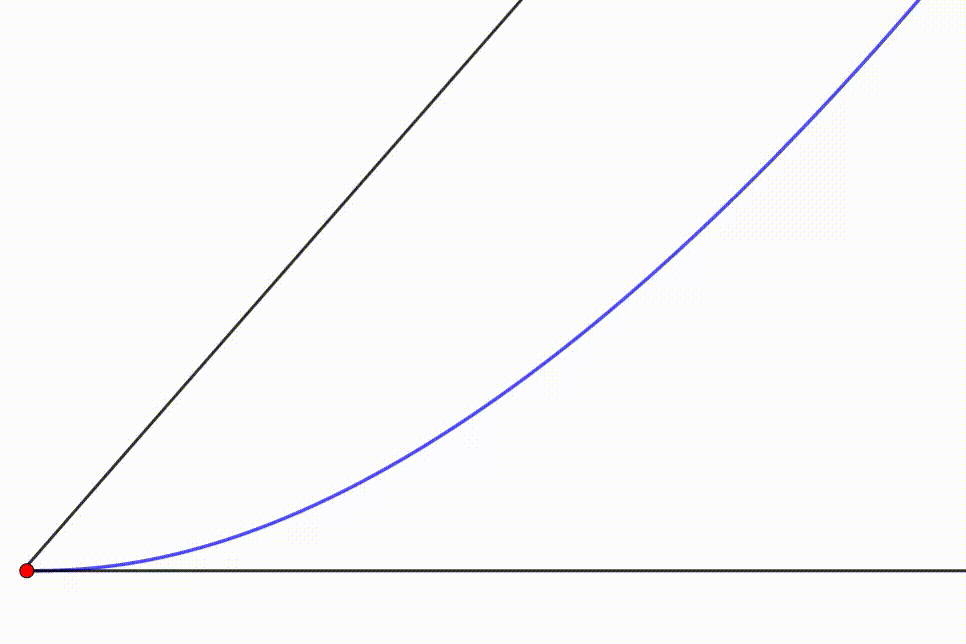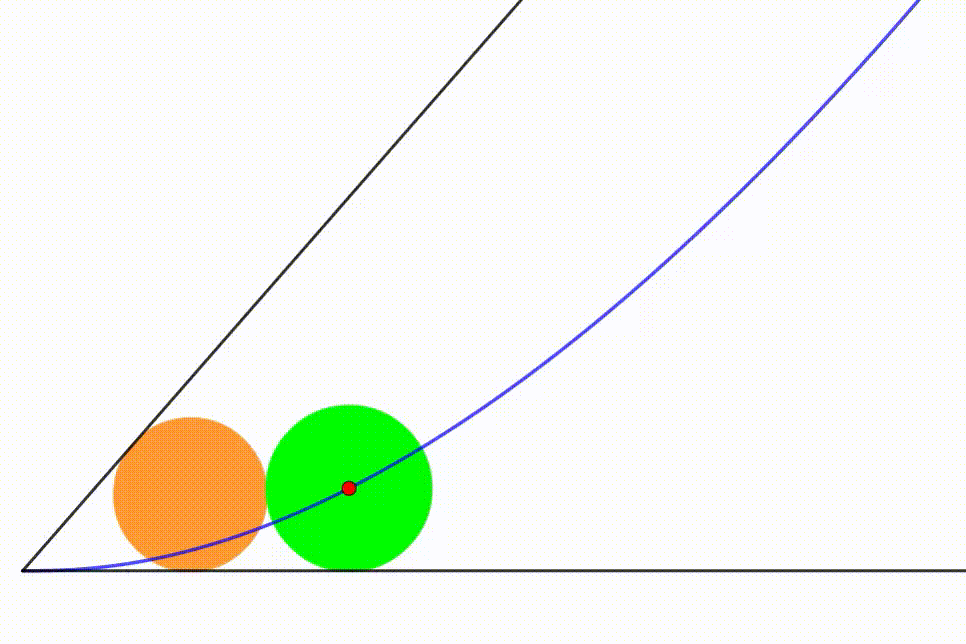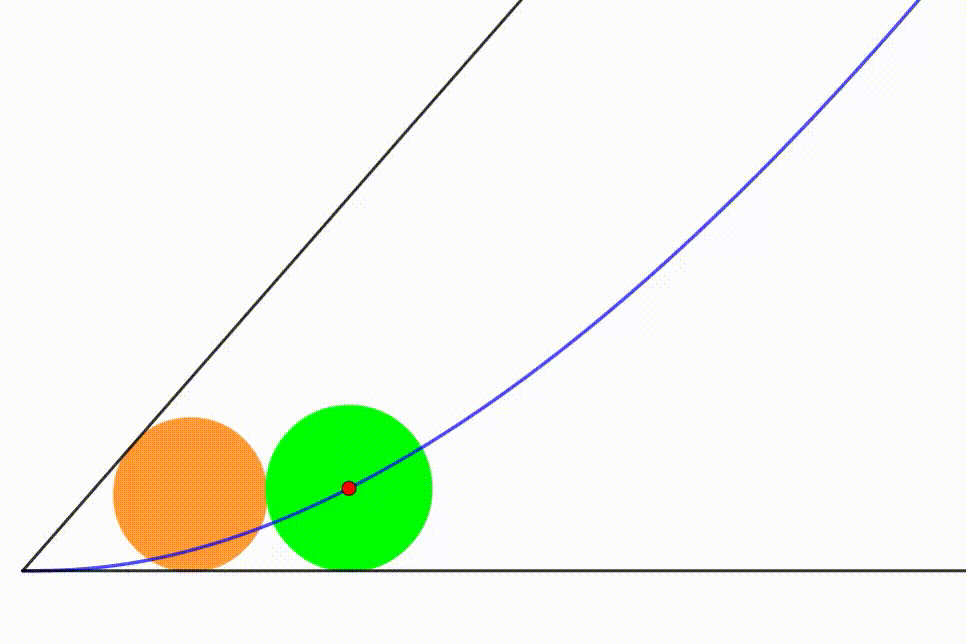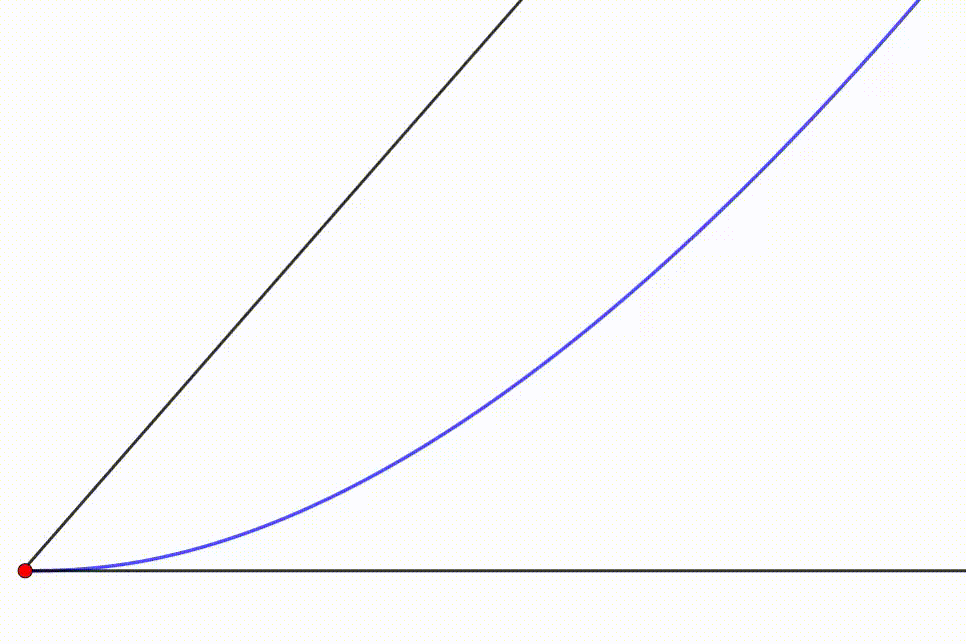 The diagram shows a black angle in which two circles are moving freely so they are tangent to the angle's sides and tangent
to each other. The measure of the black angle is
. If the radius of the orange circle is
, then the radius of the green circle has to be
at any moment. The center of the green circle traces a
locus
(blue curve). If the angle's apex is the origin of a coordinate system and the horizontal black line is the
axis, the area bounded by the line
, the blue curve and the
axis can be expressed as
, where
and
are coprime positive integers. Find
.
The diagram shows a black angle in which two circles are moving freely so they are tangent to the angle's sides and tangent
to each other. The measure of the black angle is
. If the radius of the orange circle is
, then the radius of the green circle has to be
at any moment. The center of the green circle traces a
locus
(blue curve). If the angle's apex is the origin of a coordinate system and the horizontal black line is the
axis, the area bounded by the line
, the blue curve and the
axis can be expressed as
, where
and
are coprime positive integers. Find
.
The answer is 6439.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the angle between the two black lines be θ . Then tan θ = 4 8 5 5 , sin θ = 7 3 5 5 , cos θ = 7 3 4 8 , and tan 2 θ = sin θ 1 − cos θ = 5 5 7 3 − 4 8 = 1 1 5 . We note the center of the orange circle is on the line y = 1 1 5 x . Let the center of the orange circle be ( u , r ) . Then r = 1 1 5 u . Let the center of the green circle (the red point) be P ( x , y ) . Then y = r 3 = 1 3 3 1 1 2 5 u 3 and
x = u + ( r 3 + r ) − ( r 3 − r ) = u + 2 r 2 = u + 1 2 1 5 0 u 2
Then the area bounded by the blue curve, y = 0 , and x = 1 8 is:
A = ∫ 0 1 8 y d x = ∫ 0 2 1 1 1 3 3 1 1 2 5 u 3 ( 1 + 1 2 1 1 0 0 u ) d u = 1 3 3 1 1 2 5 [ 4 u 4 + 1 2 1 2 0 u 5 ] 0 2 1 1 = 6 4 6 3 7 5 Note that x = u + 1 2 1 5 0 u 2 ⟹ d x = ( 1 + 1 2 1 1 0 0 u ) d u and u + 1 2 1 5 0 u 2 = 1 8 ⟹ u = 2 1 1
Therefore a + b = 6 3 7 5 + 6 4 = 6 4 3 9 .