Dynamic Geometry: P22

Let the center of the semicircle be the origin $O(0,0)$ of the $xy$ -plane and any point on the locus be $P(x,y)$ . Then we note that $y=r$ and

$\begin{aligned} (1-r)^2 - r^2 & = x^2 & \small \blue{\text{Since }y=r} \\ (1-y)^2 - y^2 & = x^2 \\ - 2y + 1 & = x^2 \\ \implies y & = \frac {1-x^2}2 \end{aligned}$

The equation of the locus is $y = \dfrac {1-x^2}2$ . $\rm \red{[Updated: \ ]}$ As suggested by @Thanos Petropoulos , since $f(x) =\dfrac {1-x^2}2$ is a parabola, the area bounded by the locus and the diameter is two thirds the smallest rectangle inscribing the parabola. That is $A = \dfrac 23 \times f(0) \times 2 = \dfrac 23 \times \frac 12 \times 2 = \dfrac 23$ . Therefore $a+b = 2 + 3 = \boxed 5$ .

Let’s see a purely geometric solution, not using coordinate geometry nor modern calculus, with the aid of Archimedes (although he uses the method of exhaustion, on which calculus is based).

Label the figure as follows, where the green tangent is parallel to the diameter of the semi-circle, $P$ is the center of the circle, $F$ is the center of the semi-circle, $E$ and $C$ are points of tangency and $QN$ is perpendicular to $AB$ through $P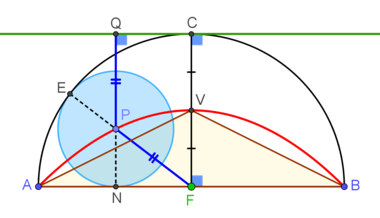$ . First we prove that the locus of the circle is part of a parabola.

Indeed,

$PF=FE-PE=FC-PN=QN-PN=PQ$ Thus, the red curve is a parabola where $F$ is its focus, the green line is its directrix and the midpoint of $FC$ , $V$ , is its vertex. We are interested in the area of the parabolic segment bounded by the parabola and its chord $AB$ .

Now, in his treatise The Quadrature of the Parabola , Archimedes proves that

The area of a parabolic segment is $\dfrac43$ that of the triangle whose base is the given chord of the parabola, and the third vertex is the point on the parabola such that the tangent to the parabola at that point is parallel to the chord.

In our case, this triangle is $VAB$ , hence,

$\text{Area of parabolic segment}=\frac{4}{3}\left[ VAB \right]=\frac{4}{3}\times \frac{1}{2}AB\cdot FV=\frac{4}{3}\times \frac{1}{2}\times 2\times \frac{1}{2}=\frac{2}{3}$ For the answer, $a=2$ , $b=3$ , thus $a+b=\boxed{5}$ .