Dynamic Geometry: P28

Both the loci are parabolas (see proof below), therefore the area bounded by them is $\dfrac 23$ the area of the blue rectangle. The height of the rectangle is $9+16 = 25$ and its width $w = 2\sqrt{25^2-7^2} = 48$ . Therefore the area enclosed by the two loci is $\dfrac 23 \times 25 \times 48 = 800$ , whose sum of digits is $\boxed 8$ .

---

Proof:

Let the center of the large circle be the origin $O(0,0)$ of the $xy$ -plane, the dividing chord is parallel to the $x$ -axis and is at a distance $h$ from $O$ . Let a point on the locus be $P(x,y)$ when the radius of the inscribed circle is $r$ . Then we note that $y = r+h$ , $\implies r = y-h$ , and:

$\begin{aligned} x^2 & = (R-r)^2 - y^2 \\ & = (R-y+h)^2 - y^2 \\ & = (R+h)^2 - 2(R+h)y + y^2 - y^2 \\ \implies y & = \frac {R+h}2 - \frac {x^2}{2(R+h)} \end{aligned}$

The equation is a parabola. Since the derivation is general, both the green and orange curves are parabolas.

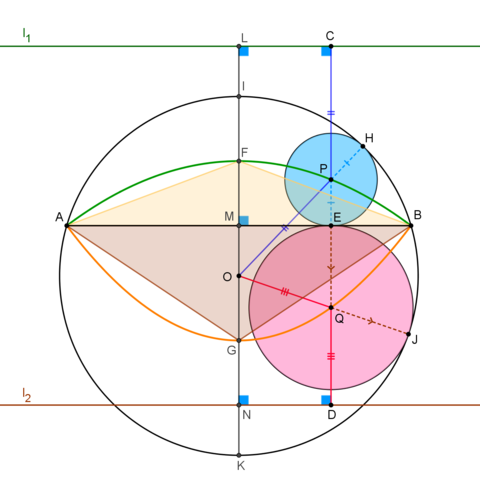Referring to the figure, $O$ is the center of the big circle, $P$ and $Q$ are the centers of the two small circles. $H$ , $J$ and $E$ are points of tangency of the circles. Line $LK$ is the perpendicular bisector of the cord $AB$ and both lines ${{l}_{1}}$ , ${{l}_{2}}$ are perpendicular to $LK$ , such that $ML=MN=R$ . $CD$ is perpendicular to $AB$ through $P$ , $E$ and $Q$ .

First we calculate the length of cord $AB$ .

By Intersecting cords theorem, $\begin{aligned} AM\cdot MB=IM\cdot MK & \Leftrightarrow A{{M}^{2}}=\left( 2R-MK \right)\cdot MK \\ & \Leftrightarrow {{\left( \frac{AB}{2} \right)}^{2}}=\left( 50-32 \right)\times 32 \\ & \Leftrightarrow AB=48 \\ \end{aligned}$

Next, we prove that the green and orange curves are parts of two parabolas.

Indeed, $OP=OH-PH=R-PE=CE-PE=CP$ Thus, the green curve is a parabola. $O$ is its focus, the green line ${{l}_{1}}$ is its directrix and the midpoint of $MI$ , $F$ , is its vertex.

Similarly, $OQ=OJ-QJ=R-QE=DE-QE=DQ$ Thus, the orange curve is also a parabola, with $O$ being its focus, line ${{l}_{2}}$ its directrix and the midpoint of $MK$ , $G$ its vertex.

The area in question is the sum of the areas of two parabolic segments bounded by the parabolas and their common cord $AB$ .

Now, in his treatise The Quadrature of the Parabola , Archimedes proves that

the area of a parabolic segment is $\dfrac43$ that of the triangle whose base is the given chord of the parabola, and the third vertex is the point on the parabola such that the tangent to the parabola at that point is parallel to the chord.

In our case, this triangles are $FAB$ and $GAB$ , hence,

$\begin{aligned} \text{Area in question} & =\frac{4}{3}\left[ FAB \right]+\frac{4}{3}\left[ GAB \right] \\ & =\frac{4}{3}\times \frac{1}{2}AB\cdot FM+\frac{4}{3}\times \frac{1}{2}AB\cdot GM \\ & =\frac{2}{3}AB\left( FM+GM \right) \\ & =\frac{2}{3}AB\left( \frac{IM}{2}+\frac{MK}{2} \right) \\ & =\frac{2}{3}AB\frac{IK}{2} \\ & =\frac{2}{3}AB\cdot R \\ & =\frac{2}{3}\times 48\times 25 \\ & =800 \\ \end{aligned}$ For the answer, the sum of the digits of the area is $\boxed{8}$ .