Dynamic Geometry: P29
 The diagram shows a unit black square. A red quarter circle is drawn using the side of the square as the radius. Two yellow semicircles are drawn. Each center moves on one square's side so the semicircles are growing, shrinking and are tangent to each other at any moment. Then, we draw a cyan circle so it's tangent to the two yellow semicircles and internally tangent to the red quarter circle. The center of the cyan circle traces a
locus
(pink curve). They area bounded by the red quarter circle and the pink curve can be expressed as:
The diagram shows a unit black square. A red quarter circle is drawn using the side of the square as the radius. Two yellow semicircles are drawn. Each center moves on one square's side so the semicircles are growing, shrinking and are tangent to each other at any moment. Then, we draw a cyan circle so it's tangent to the two yellow semicircles and internally tangent to the red quarter circle. The center of the cyan circle traces a
locus
(pink curve). They area bounded by the red quarter circle and the pink curve can be expressed as:
b π − a + b ln ( b )
where a and b are positive integers. Find the smallest a + b + ⌈ π ⌉ .
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice problem and solution! The problem says that "we draw a cyan semicircle" but it should be "we draw a cyan circle".
Log in to reply
Hi David ! Thanks a lot! I corrected the mistake. Please feel free to post your solutions to the currently unsolved problems since your approaches are always very intructive for me. Cheers!
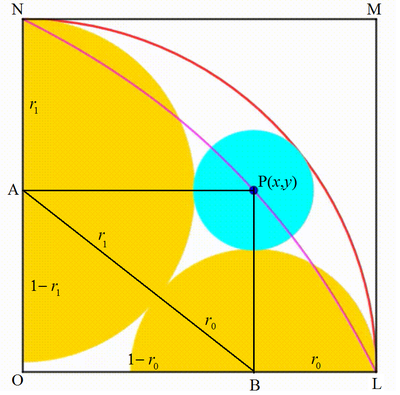
Label the unit square as L M N O , where O ( 0 , 0 ) is the origin of the x y -plane. Let an arbitrary point on the locus be P ( x , y ) , the centers and radii of the left and right semicircles be A and B and r 1 and r 0 respectively. Note that A is always at ( 0 , 1 − r 1 ) and B at ( 1 − r 0 , 0 ) . Therefore
{ x = 1 − r 0 y = 1 − r 1 ⟹ r 0 = 1 − x ⟹ r 1 = 1 − y
By Pythagorean theorem , we have:
O B 2 + O A 2 ( 1 − r 0 ) 2 + ( 1 − r 1 ) 2 1 − 2 r 0 + r 0 2 + 1 − 2 r 1 + r 1 2 2 − 2 r 0 − 2 r 1 1 − r 0 − r 1 x + y − 1 ⟹ y = A B 2 = ( r 0 + r 1 ) 2 = r 0 2 + 2 r 0 r 1 + r 1 2 = 2 r 0 r 1 = r 0 r 1 = ( 1 − x ) ( 1 − y ) = 1 − x − y + x y = 2 − x 2 ( 1 − x )
The above is the equation of the locus of P and the area bounded by the circular quadrant and the locus is given by:
A = 4 π − ∫ 0 1 y d x = 4 π − ∫ 0 1 2 − x 2 − 2 x d x = 4 π − ∫ 0 1 ( 2 − 2 − x 2 ) d x = 4 π − 2 x − 2 ln ( 2 − x ) ∣ ∣ ∣ ∣ 0 1 = 4 π − 2 + 2 ln 2 = 4 π − 8 + 4 ln 4
Therefore a + b + ⌉ π ⌉ = 8 + 4 + 4 = 4 .
See the following diagram: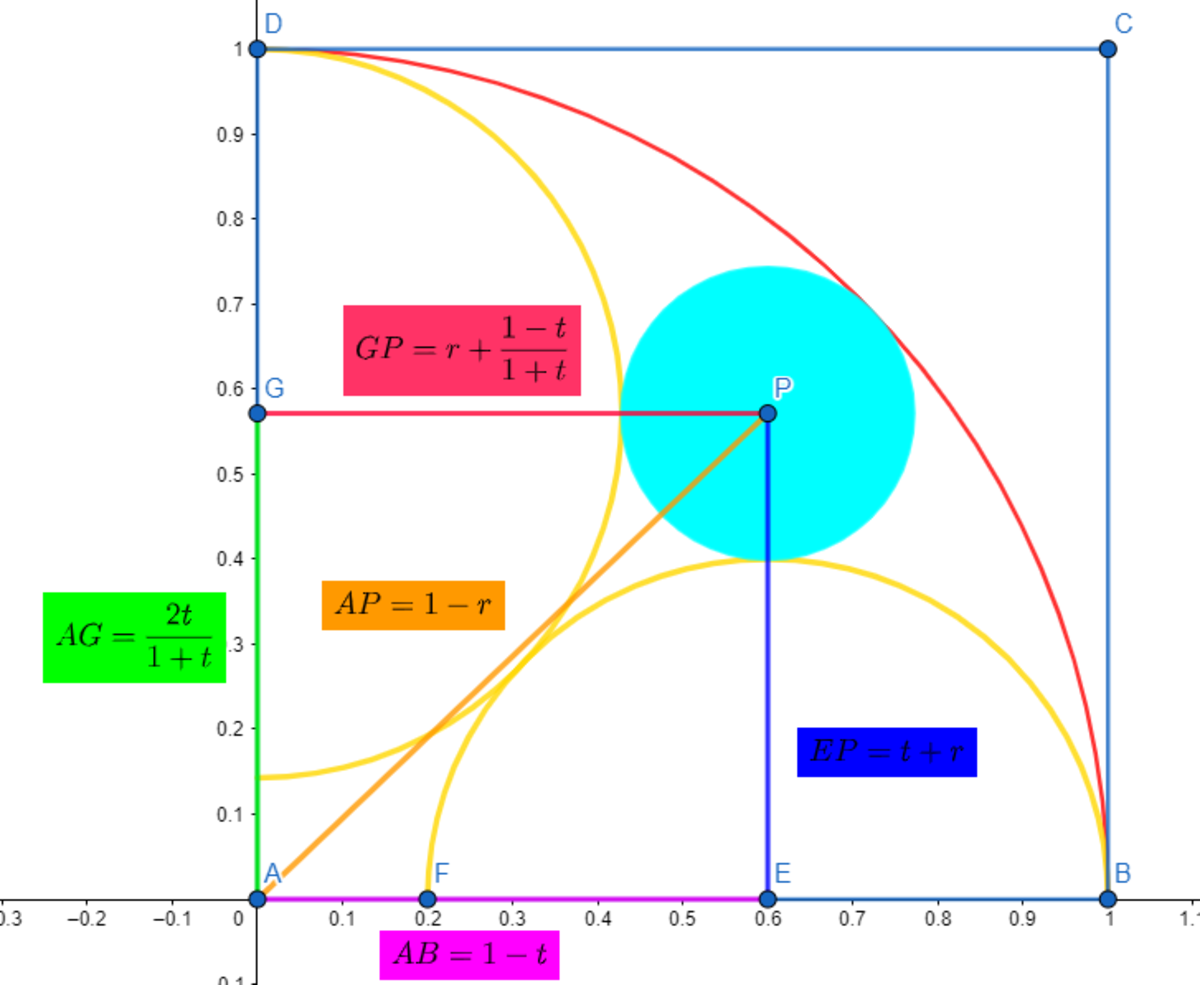
If we denote t the radius of the yellow semicircle located on the x -axis, we need to find the expression for the radius of the other yellow semicircle.
We use the Pythagoran theorem: E G 2 = A G 2 + A E 2 < = > ( 1 − D G ) 2 + ( 1 − t ) 2 = ( t + D G ) 2 < = > D G = 1 + t 1 − t , then A G = 1 + t 2 t
Now we shall find an expression for the radius of the cyan circle. Again we may use the Pythagorean theorem since there is tangency between the circle, the semicircles and the red quarter circle. We can write two equations :
⎩ ⎪ ⎨ ⎪ ⎧ ( 1 − r ) 2 = ( t + r ) 2 + ( 1 − t ) 2 ( 1 − r ) 2 = ( 1 + t 2 t ) 2 + ( 1 + t 1 − t + r ) 2
We find r = 1 + t t − t 2
We can now verify the coordinates of P the center of the cyan circle in terms of t , we get P ( 1 − t ; 1 + t t − t 2 ) after using the radius and the result are correct.
Now we can express the y coordinate of P in terms of its x coordinate, we get the equation of the locus: y = 2 − x 2 − 2 x
Finally we can evaluate the area: 4 π − ∫ 0 1 2 − x 2 − 2 x = 4 ( π − 8 + 4 ⋅ ln ( 4 ) )
So, ⌈ π ⌉ + 8 + 4 = 1 6 = 4