Dynamic Geometry: P31
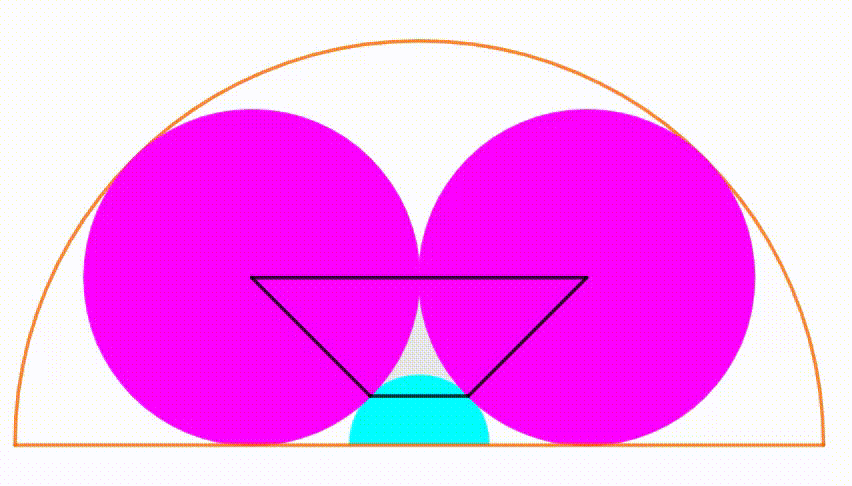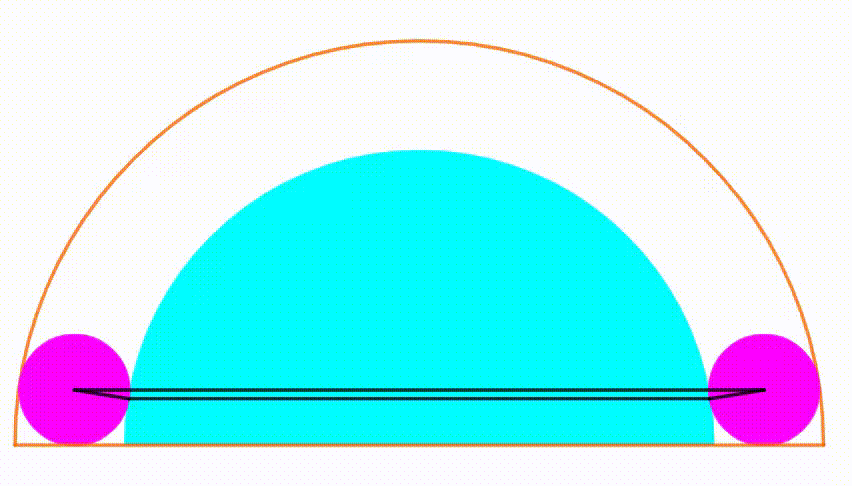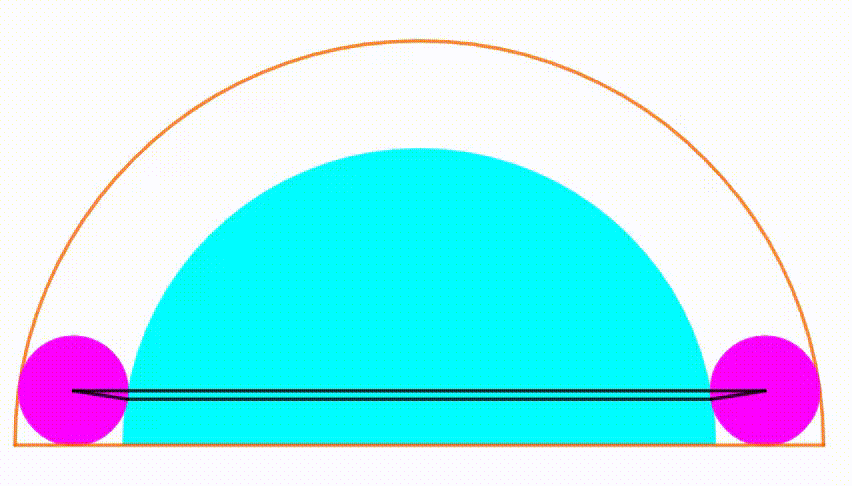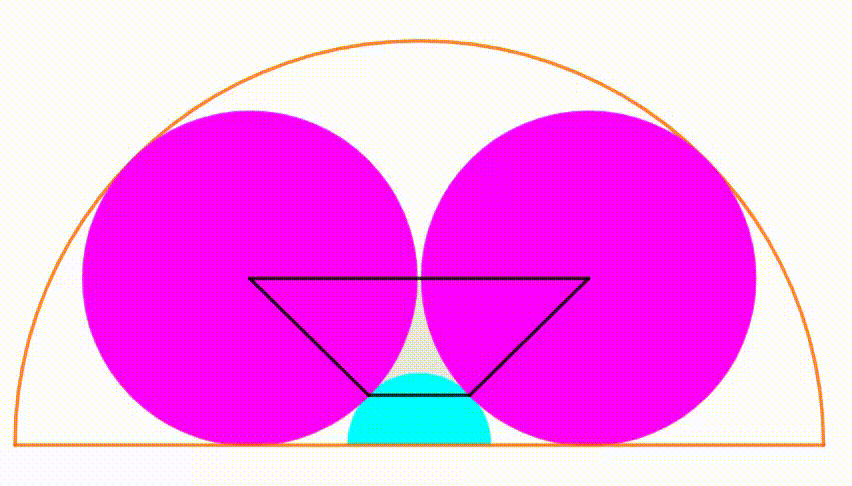 The diagram shows an orange semicircle with radius
1
. A cyan semicircle is growing and shrinking, its center and the center of the orange semicircle are the same. The two pink circles are congruent and always tangent to the cyan semicircle and internally tangent to the orange semicircle. The common points between the cyan semicircle and the pink circles are drawn. We use them and each center of the pink circle to draw a black trapezium. When its area is equal to
4
0
0
6
3
, the ratio of one pink circle's radius to the cyan semicircle's radius can be expressed as
b
a
, where
a
and
b
are coprime positive integers. Find
a
+
b
.
The diagram shows an orange semicircle with radius
1
. A cyan semicircle is growing and shrinking, its center and the center of the orange semicircle are the same. The two pink circles are congruent and always tangent to the cyan semicircle and internally tangent to the orange semicircle. The common points between the cyan semicircle and the pink circles are drawn. We use them and each center of the pink circle to draw a black trapezium. When its area is equal to
4
0
0
6
3
, the ratio of one pink circle's radius to the cyan semicircle's radius can be expressed as
b
a
, where
a
and
b
are coprime positive integers. Find
a
+
b
.
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Hello sir, thank you for taking the time to post.
@Valentin Duringer , please note that putting b a without specifications does not work because 2 3 = 1 1 . 5 = 4 6 = 6 9 = 3 4 . 5 = ⋯ also − 2 − 3 = − 1 − 1 . 5 = − 4 − 6 = − 6 − 9 = − 3 − 4 . 5 = ⋯ . There are infinitely many answers to a + b .
Let the center of the large and cyan semicircle be O ( 0 , 0 ) , the origin of the x y -plane, Q ( x q , y q ) be the center of the right pink circle, and P ( x p , y p ) , the tangent point of the cyan semicircle and the right pink circle. Let the radii of the large semicircle, the cyan semicircle, and the pink circle be 1 , r 1 , and r 2 respectively.
We note that r 1 + 2 r 2 = 1 . Let k = r 1 r 2 ⟹ r 2 = k r 1 . Then r 1 + 2 k r 1 = 1 ⟹ r 1 = 1 + 2 k 1 .
We also note that y q = r 2 and by Pythagorean theorem :
x q 2 + y q 2 x q 2 + r 2 2 x q 2 + k 2 r 1 2 x q 2 ⟹ x q = ( r 1 + r 2 ) 2 = r 1 2 ( 1 + k ) 2 = r 1 2 ( 1 + 2 k + k 2 ) = r 1 ( r 1 + 2 k r 1 ) = r 1 = r 1 Note that r 1 + 2 k r 1 = 1
By similar triangles , x q x p = r 1 + r 2 r 1 = 1 + k 1 ⟹ x p = 1 + k r 1 and y p = 1 + k k r 1 .
The area of the trapezoid is given by:
2 2 x q + 2 x p ⋅ ( y q − y p ) ( r 1 + 1 + k r 1 ) ( k r 1 − 1 + k k r 1 ) ( 1 + k ) 2 k 2 r 1 2 3 ( 2 + k ) ( 1 + 2 k ) 2 3 ( 1 + k ) 2 k 2 ( 2 + k ) ⟹ k = 4 0 0 6 3 = 4 0 0 6 3 = 4 0 0 6 3 = 4 0 0 6 3 = 2 3
Therefore a + b = 3 + 2 = 5 .