Dynamic Geometry: P32

Let the center of the large semicircle be $O(0,0)$ , the origin of the $xy$ -plane and its radius $1$ . Let the red line be $x=u$ , the radii of the pink, yellow, cyan, and green circle be $r_1$ , $r_2$ , $r_3$ , and $r_4$ respectively. Let the centers of the cyan and green circles be $P(x_p, y_p)$ and $Q(x_q,$ respectively. Then the distance between the blue and green points $D = |y_p-y_q|$ . We note that $x_p = u+r_3$ and $y_p = \sqrt{(r_1+r_3)^2-(r_1-r_3)^2} = 2\sqrt{r_1r_3}$ . Similarly, $x_q = u-r_4$ and $y_q = 2\sqrt{r_2r_4}$ .

Let us find the four radii in terms of $u$ . $r_1 = \dfrac {1-u}2$ , $r_2 = \dfrac {1+u}2$ , and

$\begin{aligned} x_p^2+y_p^2 & = (1-r_3)^2 \\ (u+r_3)^2 + (2\sqrt{r_1r_3})^2 & = 1 -2r_3 + r_3^2 \\ u^2 + 2ur_3 + r_3^2 + \blue{4r_1} r_3 & = 1 -2r_3 + r_3^2 & \small \blue{\text{Note that }r_1 = \frac {1-u}2} \\ u^2 + 2ur_3 + r_3^2 + \blue{(2-2u)} r_3 & = 1 -2r_3 + r_3^2 \\ u^2 + 2r_3 & = 1 - 2r_3 \\ \implies r_3 & = \frac {1-u^2}4 \end{aligned}$

Similarly, $r_4 = \dfrac {1-u^2}4 = r_3$ . Without loss of generality, assume that $y_q > y_p$ . Then

$\begin{aligned} D & = y_q - y_p = 2\sqrt{r_2r_4} - 2\sqrt{r_1r_3} = \frac {(1+u)\sqrt{1-u}-(1-u)\sqrt{1+u}}{\sqrt 2} \end{aligned}$

To find the maximum value of $D$ ,

$\begin{aligned} \frac {dD}{du} & = \frac 1{\sqrt 2} \left(\sqrt{1-u} - \frac {1+u}{2\sqrt{1-u}} + \sqrt{1+u} - \frac {1-u}{2\sqrt{1+u}}\right) \quad \quad \small \blue{\text{Putting }\frac {dD}{du}=0} \\ \sqrt{1+u} + \sqrt{1-u} & = \frac {1+u}{2\sqrt{1-u}} + \frac {1-u}{2\sqrt{1+u}} \\ 2\sqrt{1-u^2} \left(\sqrt{1+u} + \sqrt{1-u}\right) & = \blue{(1+u)^\frac 32 + (1-u)^\frac 32} \quad \quad \small \blue{\text{Since }a^3 + b^3 = (a+b)(a^2 - ab + b^2)} \\ 2\sqrt{1-u^2} \left(\sqrt{1+u} + \sqrt{1-u}\right) & = \blue{\left(\sqrt{1+u} + \sqrt{1-u}\right) \left(1+u - \sqrt{1-u^2} + 1-u \right)} \\ 2\sqrt{1-u^2} & = 2 - \sqrt{1-u^2} \\ 3\sqrt{1-u^2} & = 2 \\ 1 - u^2 & = \frac 49 \\ \implies u & = \frac {\sqrt 5}3 \end{aligned}$

Therefore $D$ is maximum when $u = \frac {\sqrt 5}3$ , since minimum $D$ is $0$ as can be seen from the animation. Then $r_1 = \frac {3-\sqrt 5}6$ , $r_2 = \frac {3+\sqrt 5}6$ , and $r_3 = r_4 = \frac 19$ . And the fraction of white area:

$\begin{aligned} \frac {\pi \left(\frac 12 - \frac {r_1^2}2 - \frac {r_2^2}2 - r_3^2-r_4^2\right)}{\frac \pi 2} = 2\left(\frac 12 - \frac {14-6\sqrt 5}{72} - \frac {14+6\sqrt 5}{72} - \frac 2{81} \right) = \frac {14}{81} \end{aligned}$

Therefore $a+b = \boxed{95}$ .

Label the diagram as follows:

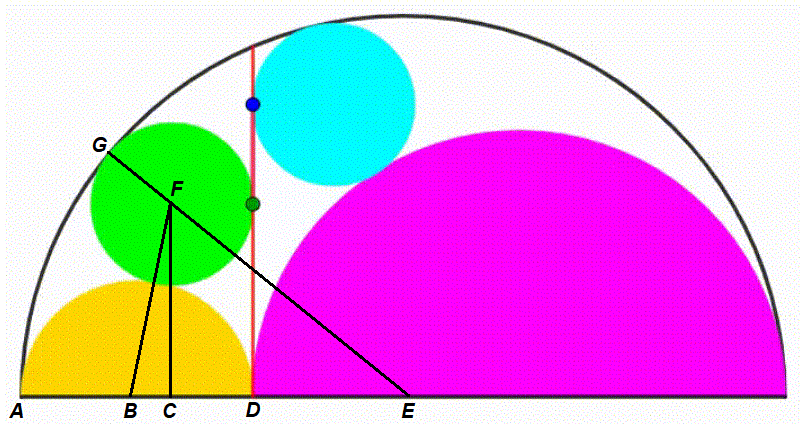
Let the radius of the black semi-circle be $1$ , the radius of the yellow semi-circle be $r$ , the radius of the green circle be $s$ , and $\angle FBC$ be $\theta$ .

Since $BC = BD - CD = r - s$ and $BF = r + s$ , from $\triangle BCF$ we know that $\cos \theta = \cfrac{BC}{BF} = \cfrac{r - s}{r + s}$ .

Since $BE = AE - AB = 1 - r$ , $FE = GE - GF = 1 - s$ , and $BF = r + s$ , by the law of cosines on $\triangle BEF$ we know that $\cos \theta = \cfrac{BE^2 + BF^2 - FE^2}{2 \cdot BE \cdot BF} = \cfrac{(1 - r)^2 + (r + s)^2 - (1 - s)^2}{2 \cdot (1 - r) \cdot (r + s)} = \cfrac{r^2 + rs - r + s}{(1 - r)(r + s)}$ .

Therefore, $\cos \theta = \cfrac{r - s}{r + s} = \cfrac{r^2 + rs - r + s}{(1 - r)(r + s)}$ , which solves to $s = r(1 - r)$ .

By the Pythagorean Theorem on $\triangle BCF$ , $CF = \sqrt{BF^2 - BC^2} = \sqrt{(r + s)^2 - (r - s)^2} = 2\sqrt{rs}$ . Substituting $s = r(1 - r)$ gives $CF = 2r\sqrt{1 - r}$ , which is also the height of the green dot.

Let the radius of the pink semi-circle be $q$ and the radius of the cyan circle be $t$ .

Then by similar arguments as above, $t = q(1 - q)$ and the height of the blue dot will be $2q\sqrt{1 - q}$ .

From the diameter of the black semi-circle, $2r + 2q = 2$ , which solves to $q = 1 - r$ .

Substituting $q = 1 - r$ into $t = q(1 - q)$ and $2q\sqrt{1 - q}$ gives $t = r(1 - r) = s$ and a blue dot height of $2(1 - r)\sqrt{r}$ .

The distance between the blue and green point is then $y = 2r\sqrt{1 - r} - 2(1 - r)\sqrt{r}$ , which reaches a maximum when its derivative is equal to $0$ , or when $\cfrac{dy}{dr} = \cfrac{\sqrt{r}(2 - 3r) + \sqrt{1 - r}(3r - 1)}{\sqrt{r(1 - r)}} = 0$ , which solves to $r = \cfrac{3 \pm \sqrt{5}}{6}$ .

If $r = \cfrac{3 \pm \sqrt{5}}{6}$ , then $q = 1 - r = \cfrac{3 \mp \sqrt{5}}{6}$ , and $s = t = r(1 - r) = \cfrac{1}{9}$ .

The fraction of the white area is then $\cfrac{\frac{1}{2} \pi 1^2 - (\frac{1}{2}\pi q^2 + \frac{1}{2}\pi r^2 + \pi s^2 + \pi t^2)}{\frac{1}{2} \pi 1^2} = 1 - q^2 - r^2 - 4s^2 = 1 - \bigg(\cfrac{3 \mp \sqrt{5}}{6} \bigg)^2 - \bigg(\cfrac{3 \pm \sqrt{5}}{6} \bigg)^2 - 4\bigg(\cfrac{1}{9} \bigg)^2 = \cfrac{14}{81}$ .

Therefore, $a = 14$ , $b = 81$ , and $a + b = \boxed{95}$ .