Dynamic Geometry: P33
 The diagram shows a black circle. We draw its diameter in green. Then we draw two orange segments perpendicular to each other. The green diameter is the angle bisector of the angle formed by the orange segments. The red point is moving freely along the green diameter. We draw to cyan circles. A cyan circle is internally tangent to the black circle and to the orange segments. The center of each cyan circle traces a
locus
(pink curve). The ratio of the
maximum
area of one cyan circle to the area bounded by the two pink curves can be expressed as:
The diagram shows a black circle. We draw its diameter in green. Then we draw two orange segments perpendicular to each other. The green diameter is the angle bisector of the angle formed by the orange segments. The red point is moving freely along the green diameter. We draw to cyan circles. A cyan circle is internally tangent to the black circle and to the orange segments. The center of each cyan circle traces a
locus
(pink curve). The ratio of the
maximum
area of one cyan circle to the area bounded by the two pink curves can be expressed as:
b π − c ( d b − c ) π
where d , b and c are positive integers and b is square-free. Find the smallest d + b + c .
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
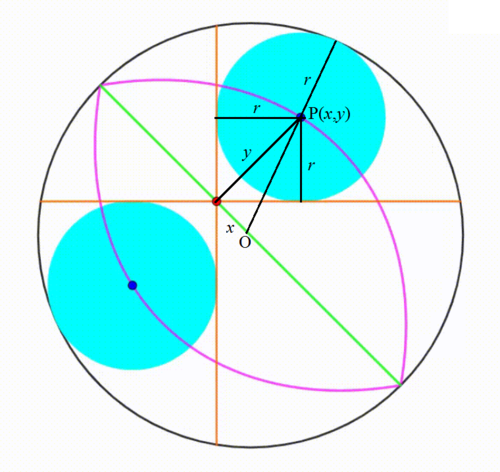
Let the radius of the big circle (I don't see much black but white) be 1 and its center be O ( 0 , 0 ) of the x y -plane with the slanting green line (Does a circle has a diagonal?) as the x -axis. Turn you head 4 5 ∘ and I will show you not only we can prove that the pink locus is part of an ellipse but how.
Let an arbitrary point on the locus be P ( x , y ) and the radius of the circle be r when P is the center of the variable circle (yah, I know it is cyan, but to be politically-correct to the color-vision impaired). By Pythagorean theorem we have:
{ x 2 + y 2 = O P 2 = ( 1 − r ) 2 y 2 = r 2 + r 2 = 2 r 2 . . . ( 1 ) . . . ( 2 )
( 1 ) : x 2 + y 2 x 2 + y 2 x 2 + 2 y 2 + 2 y x 2 + ( 2 y + 1 ) 2 2 x 2 + 4 ( y + 2 ) 2 = r 2 − 2 r + 1 = 2 y 2 − 2 y + 1 = 1 = 2 = 1 From ( 2 ) : r = 2 y
See! The locus is the top part of an ellipse with center at ( 0 , − 2 ) , minor-axis a = 2 and major-axis b = 2 (Note that a and b has nothing to do with the answer option a + b + c . Of course this work out to be y = 4 − 2 x 2 − 2 as shown by @Valentin Duringer , and we can find the area bounded the two curves by using 2 ∫ − 1 1 y d x . But since it is an ellipse, we can apply:
⎩ ⎪ ⎨ ⎪ ⎧ 2 x 2 = cos 2 θ 4 ( y + 2 ) 2 = sin 2 θ ⟹ x = 2 cos θ ⟹ y = 2 sin θ − 2
And if you don't want to find the definite integral using Wolfram Alpha or other software, you can do as below:
A = 2 ∫ − 1 1 y d x = 4 ∫ 0 1 y d x = 4 ∫ 2 π 4 π ( 2 sin θ − 2 ) ( − 2 sin θ ) d θ = ∫ 4 π 2 π ( 8 2 sin 2 θ − 8 sin θ ) d θ = ∫ 4 π 2 π ( 4 2 ( 1 − cos 2 θ ) − 8 sin θ ) d θ = 4 2 θ − 2 2 sin 2 θ + 8 cos θ ∣ ∣ ∣ ∣ 4 π 2 π = 2 π + 2 2 − 4 2 = 2 π − 2 2 Since y is even. As d x = − 2 sin θ
The largest variable circle is when x = 0 , ⟹ θ = 2 π , y = 2 − 2 , and r = 2 − 1 . Then the area of the largest variable circle A ◯ = π ( 2 − 1 ) 2 = ( 3 − 2 2 ) π . And the ratio:
A A ◯ = 2 π − 2 2 ( 3 − 2 2 ) π = 2 π − 4 ( 3 2 − 4 ) π
Then the require answer (I can't mention a and b because I have mentioned them for other purposes) is 3 + 2 + 4 = 3 . (Sorry for my sarcasm, I'm just trying to be a more serious amateur math nerd.)
A lot of sarcasm indeed (even my figure is not safe from it!) but I'm getting used to it, you could have innovated by putting a "confused" after my solution and sarcasm would become contempt, it would have been even funnier ! Thank you for posting anyway. I amended the problems where I could the solve the "a" issue.
Log in to reply
Glad that you can still stand me. Anyway, there are still problems you didn't end with a full-stop.
Note that sides of △ A B C in all texts are always a , b , and c . If you notice, I put a comma after b . This is because the bloody Americans need that comma while the British do not. Since this website is American I use the US English like "color" instead of "colour", "center" instead of "centre", "trapezoid" instead of "trapezium". Also I notice the Continental Europeans use comma as decimal while the English-speaking world uses a dot. The reverse for the thousand notation. I think that is why you use semicolon ";" for coordinates ( x ; y ) but the bloody English-speaking world uses comma ( x , y ) . Have a great day.
@Chew-Seong Cheong , I amended the problems. Do not worry, I will even pay an hommage to your mentoring when I'll publish problem number 100 of the series...
See the following diagram: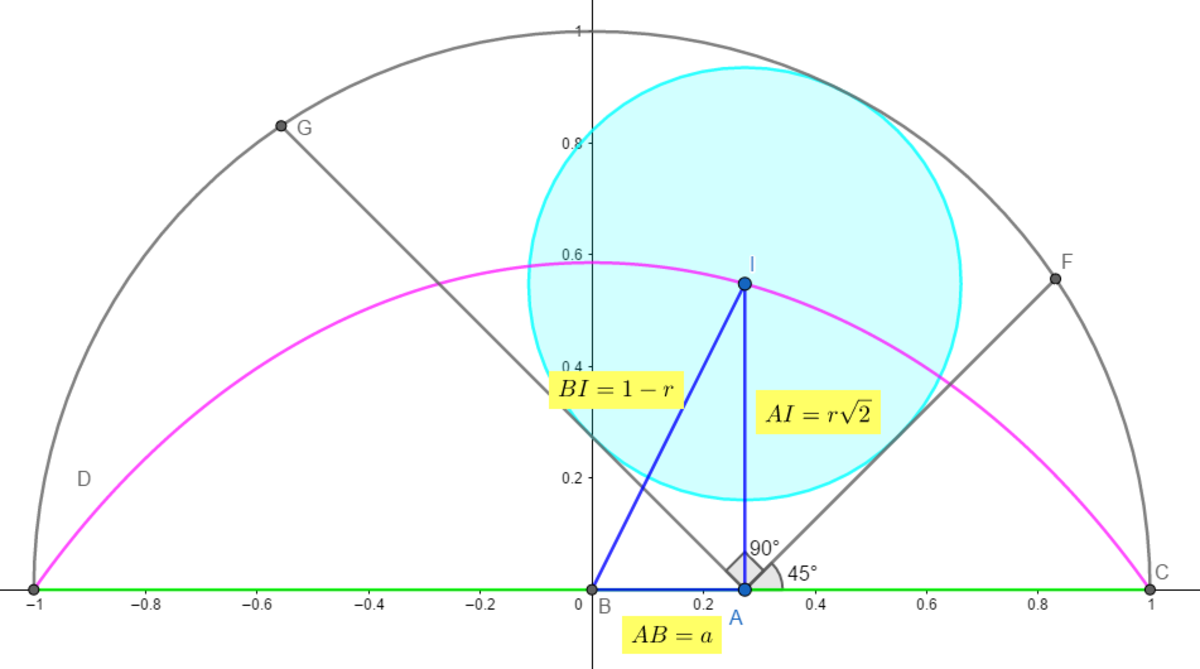 - The moving red point is point
A
(
a
;
0
)
on our diagram. We set the radius of the circle as
1
- The moving red point is point
A
(
a
;
0
)
on our diagram. We set the radius of the circle as
1
We use the pythagorean theorem to express the radius r of the cyan circle in terms of a
We need to solve the equation: 2 r 2 + a 2 = ( 1 − r ) 2 < = > r = 2 − a 2 − 1
We know that the center of the cyan circle has coordinates ( a ; r 2 ) which after substitution becomes ( a ; 4 − 2 a 2 − 2 )
Having the x and y coordinate of the center in terms of a , we use substitution to get y in terms of x to get the equation of the locus.
We get: y = 4 − 2 x 2 − 2
Obviously the area of the cyan circle is its maximum when point A has coordinates ( 0 ; 0 ) . The area is then: π ( 3 − 2 2 )
Now we evaluate the area bounded by the two pink curves: 2 ⋅ ∫ − 1 1 4 − 2 x 2 − 2 = 2 2 π − 4
Then we evaluate the ratio between those areas and get: 2 π − 4 π ( 3 2 − 4 )
d = 3 , b = 2 , c = 4 and ∣ ∣ 3 + 2 + 4 ∣ ∣ = ∣ ∣ 9 ∣ ∣ = 3