Dynamic Geometry: P34
 The diagram shows a blue semicircle with radius
1
. A red point is moving freely along the semicircle's symmetry axis. We draw two green segments starting from the edges of the semicircle's diameter and going throught the red points. This allows us the inscribe
4
circles. We use the center of each circle to drawn a black quadrilateral. When the area of the black quadrilateral is equal to
1
4
4
2
5
, the ratio of the cyan circle's radius to the radius of the yellow circle can be expressed as
b
c
where
c
and
b
are coprime positive integers. Find
c
+
b
.
The diagram shows a blue semicircle with radius
1
. A red point is moving freely along the semicircle's symmetry axis. We draw two green segments starting from the edges of the semicircle's diameter and going throught the red points. This allows us the inscribe
4
circles. We use the center of each circle to drawn a black quadrilateral. When the area of the black quadrilateral is equal to
1
4
4
2
5
, the ratio of the cyan circle's radius to the radius of the yellow circle can be expressed as
b
c
where
c
and
b
are coprime positive integers. Find
c
+
b
.
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Valentin Duringer , avoid using a , b , and c in answer format in geometry problems. This is because a , b , and c are commonly used in triangle sides, a and b the semi-axes of and ellipse, a , b , and c as terms of arithmetic and geometric progressions. Usually members use q p . If three terms are needed can use u , v , and w or k , m , and n . For more k , m , n , p , q or α , β , γ , δ , ...
Thank you for including that wiki on tangent substitution.
See the diagram below:
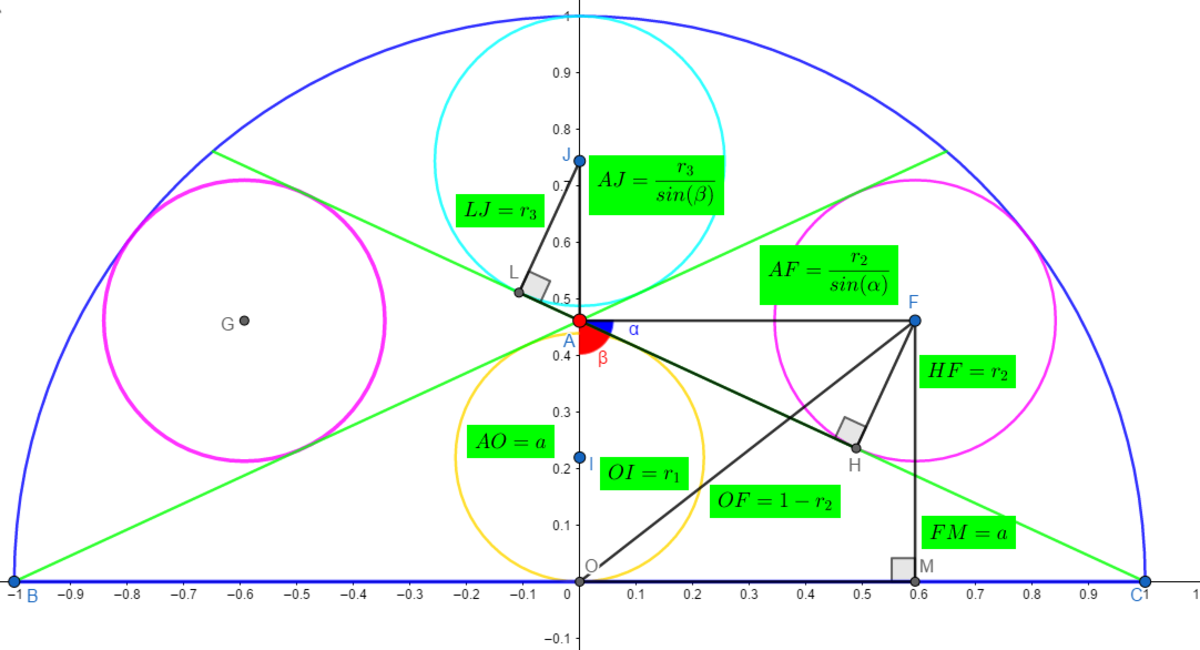
-
Point A ( 0 ; a ) is our parameter in this problem. First, we shall evaluate r 1 , the inradius of triangle A B C .
-
We get r 1 = p e r i m e t e r 2 ⋅ A r e a = A C + A B + B C A O ⋅ O B = 2 + 2 ⋅ a ² + 1 2 ⋅ a = 1 + a ² + 1 a
-
Now we use the pytagorean theorem and basic trigonometry to get r 2 , with α = 9 0 ° − β
-
We get sin ( α ) = cos ( 9 0 ° − α ) = cos ( β ) = a 2 + 1 a and sin ( α ) = A F H F
-
We combine those two equations and get a 2 + 1 a = A F r 2 < = > A F = a a 2 + 1 ⋅ r 2
-
Now by the Pythagorean theorem: O F 2 = A F 2 + F M 2 < = > ( 1 − r 2 ) 2 = A F 2 + a 2 < = > A F = ( 1 − r 2 ) 2 − a 2
-
We combine the two expressions for A F and get: r 2 = a − a 2
-
Let's get r 3 . We use a similar method, it's even easier since the center is on the y axis.
-
We get r 3 = 1 + 1 + a 2 1 − a
-
Diving the black quadrilateral into two isosceles triangles, its area, after some algebra, can be expressed as: A F ⋅ ( A J + A I ) = 1 + 1 + a 2 ∣ − 1 + a ∣ ( 1 + a 2 )
-
Now we solve 1 + 1 + a 2 ∣ − 1 + a ∣ ( 1 + a 2 ) = 1 4 4 2 5
-
We get a = 4 3 and evaluate r 2 r 3 and we obtain 3 1
-
Finally ∣ ∣ c + b ∣ ∣ = ∣ ∣ 1 + 3 ∣ ∣ = 2
This is my favorite solution of yours so far, especially because of this line: r 2 = a − a 2
Log in to reply
Indeed, sometimes the value for the radius is quit elegant, I have a lot more problems where the value is cute, stay tuned
Label the semicircle A B C , where A B is its diameter and C its highest point; the centers of the semicircle, yellow, cyan, and pink circles, O , P , Q , S and T respectively; and the red point R . Let the radii of the yellow, cyan, and pink circles be r 1 , r 2 , and r 3 respectively, and ∠ R A O = ∠ R B O = θ .
We note that A O O P = r 1 = tan 2 θ = t (my favorite half-angle tangent substitution ). Let O R = v = tan θ = 1 − t 2 2 t . If we extend the two green segments to meet the tangent to the semicircle at C , we note that the cyan and yellow circles are inscribed in two similar triangles. The ratio of their radii is the ratio of their heights. Therefore r 2 = v 1 − v ⋅ r 1 = 2 1 − 2 t − t 2 .
Because of symmetry, S , R , and T are colinear and S T ∣ ∣ A B . By Pythagorean theorem, we note that:
O R 2 + R T 2 v 2 + ( r 3 csc θ ) 2 v 2 + r 3 2 ( 1 + cot 2 θ ) v 2 + v 2 r 3 2 v 2 r 3 2 + 2 r 3 + v 2 ( v r 3 + v ) 2 ⟹ r 3 = O T 2 = ( 1 − r 3 ) 2 = 1 − 2 r 3 + r 3 2 = 1 − 2 r 3 = 1 = 1 = v ( 1 − v ) = ( 1 − t 2 ) 2 2 t ( 1 − 2 t − t 2 ) Note that R T = R S = r 3 csc θ Note that v = tan θ
The area of the quadrilateral P S Q T is given by P Q ⋅ R S and when it is 1 4 4 2 5 , we have:
( 1 − r 1 − r 2 ) r 3 csc θ ( 1 − t − 2 1 − 2 t − t 2 ) ⋅ ( 1 − t 2 ) 2 2 t ( 1 − 2 t − t 2 ) ⋅ 2 t 1 + t 2 2 ( 1 − t 2 ) 2 ( 1 + t 2 ) 2 ( 1 − 2 t − t 2 ) t 4 − 2 t 2 + 1 − ( t 6 + 2 t 5 + t 4 + 4 t 3 − t 2 + 2 t − 1 ) 7 2 t 6 + 1 4 4 t 5 + 9 7 t 4 + 2 8 8 t 3 − 1 2 2 t 2 + 1 4 4 t − 4 7 ( 3 t − 1 ) ( 2 4 t 5 + 5 6 t 4 + 5 1 t 3 + 1 1 3 t 2 − 3 t + 4 7 = 1 4 4 2 5 = 1 4 4 2 5 = 1 4 4 2 5 = 7 2 2 5 = 0 = 0
There is a positive root t = 3 1 . Then the ratio r 1 r 2 = 2 t 1 − 2 t − t 2 = 6 9 − 6 − 1 = 3 1 . Therefore the required answer is 1 + 3 = 2 .