Dynamic Geometry: P35
The diagram shows a blue circle with radius
. A yellow and a pink semicircle are tangent to each other and internally tangent to the blue circle. They are freely moving and shrinking/gowing along the blue circle's horizontal axis. Each green circle is tangent to the blue circle and to the changing semicircles. We use the center of each green circle and semicircles to draw a black quadrilateral. When the area of the black quadrilateral is equal to
, the ratio of the radius of the smallest semicircle to the radius of the largest semicircle can be expressed as
where
and
are coprime positive integers. Find
.
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
See the diagram below: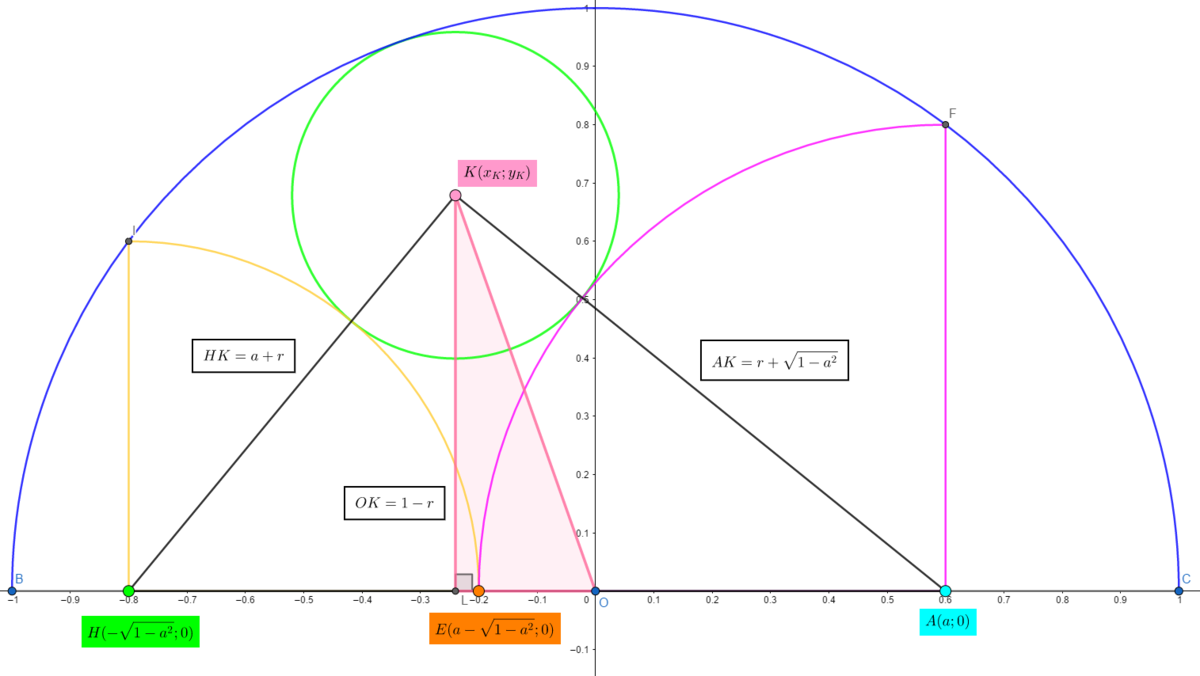
- The figure is easy to make when you know that in this kind of configuration, the sum of the areas of the two semicircles is always equal to half the area of the circle.
Let us find x K , y K and r . Altough, only y K is relevant here.
We use the pythagorean theorem to write three equations:
⎩ ⎪ ⎨ ⎪ ⎧ ( a + r ) 2 = ( x K + 1 − a 2 ) 2 + y K 2 ( 1 − a 2 + r ) 2 = ( x K − a ) 2 + y K 2 ( 1 − r ) 2 = x K 2 + y K 2
⎩ ⎪ ⎨ ⎪ ⎧ x K = 2 1 ( − 1 + a + 2 a 2 − 1 − a 2 ) y K = 2 a − a 2 + 1 r = 2 1 ( 1 − a − 1 − a 2 + 2 a 1 − a 2 )
Now we can evaluate the area of the quadrilateral which is equal to: K E ⋅ A H = 2 − a 2 ( − 1 + a 2 ) ( a + 1 − a 2 )
We can solve 2 − a 2 ( − 1 + a 2 ) ( a + 1 − a 2 ) = 1 2 5 8 4 2 and we find a = 5 3 or a = 5 4 which does not matter for the final result, both values will work.
If a = 5 3 , then 1 − a 2 = 5 4 ) and the ratio of the largest to the smallest radius is equal to 3 4
Finally 3 + 4 = 7