Dynamic Geometry: P38
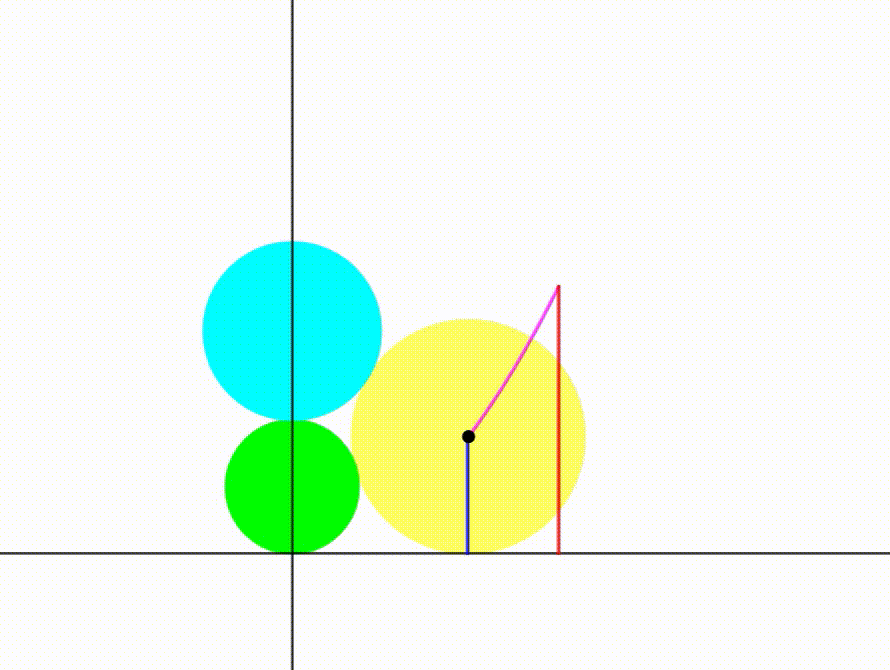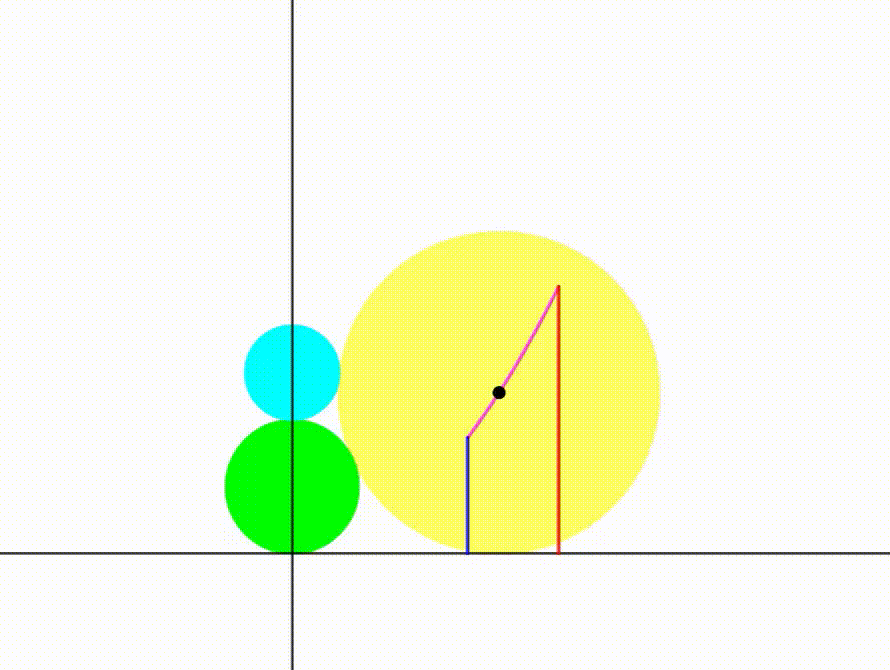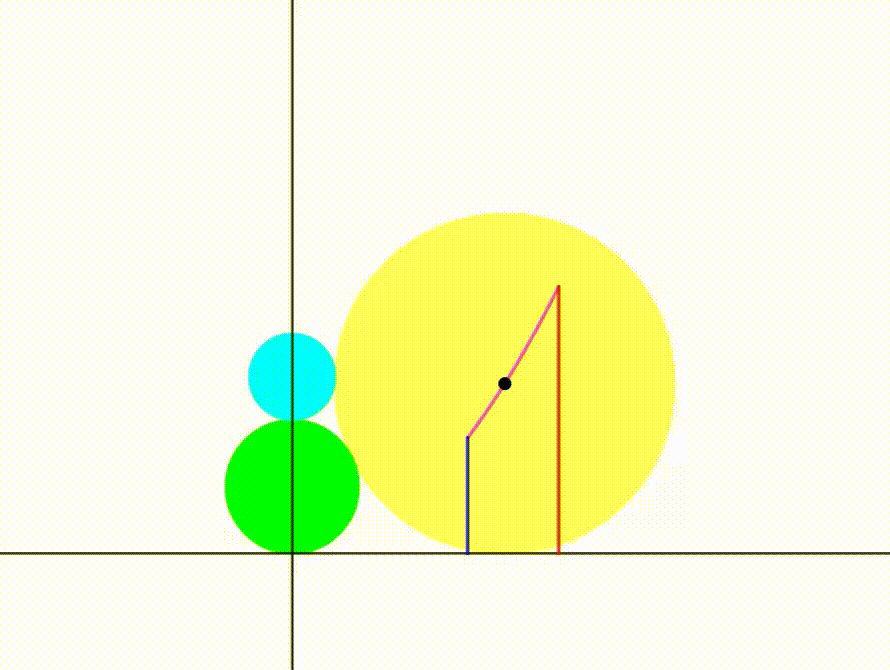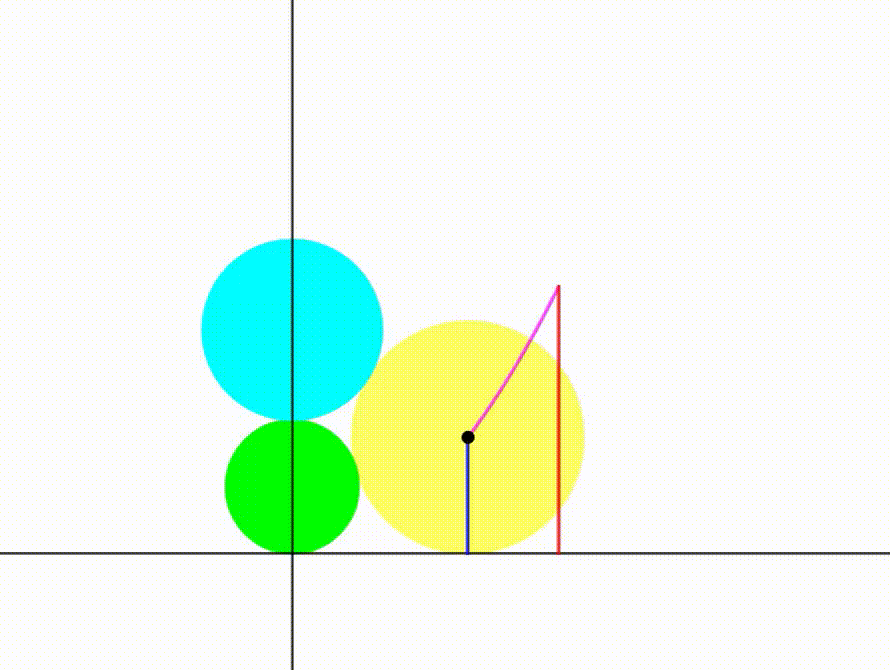 The diagram shows a green circle with radius
1
, its center has coordinates
(
0
;
1
)
. The cyan circle has radius
r
, its center has coordinates
(
0
;
2
+
r
)
. A yellow circle is drawn so it's tangent to the
x
axis, to the green circle and to the cyan circle at any moment. The center of the yellow circle traces a
locus
(pink curve). Its center bounces between a blue vertical segment and a red vertical segment. When the center touches the red segment, its
y
and
x
coordinates are equal. When the center touches the blue segment, the radius of the three circles are in arithmetic progression (the green circle shall be the smallest and the yellow the largest circle). The area bounded by the pink curves and the two vertical segments can be expressed as:
The diagram shows a green circle with radius
1
, its center has coordinates
(
0
;
1
)
. The cyan circle has radius
r
, its center has coordinates
(
0
;
2
+
r
)
. A yellow circle is drawn so it's tangent to the
x
axis, to the green circle and to the cyan circle at any moment. The center of the yellow circle traces a
locus
(pink curve). Its center bounces between a blue vertical segment and a red vertical segment. When the center touches the red segment, its
y
and
x
coordinates are equal. When the center touches the blue segment, the radius of the three circles are in arithmetic progression (the green circle shall be the smallest and the yellow the largest circle). The area bounded by the pink curves and the two vertical segments can be expressed as:
b a ( a b − b a × a b )
where a and b are coprime positive integers. Find a + b .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
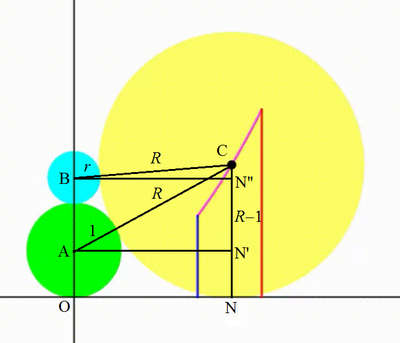
Label the origin as O , the centers of the green, cyan, and yellow circles be A , B , and C . Let C N be perpendicular to the x -axis, and A N ′ and B n " be parallel to O N . We note that O N = A N ′ = B N " = ℓ . Let the radius of the yellow circle be R . By Pythagorean theorem ,
A C 2 − C N ′ 2 ( R + 1 ) 2 − ( R − 1 ) 2 ⟹ 4 R = A N ′ 2 = ℓ 2 = ℓ 2
SImilarly,
B C 2 − C N " 2 ( R + r ) 2 − ( R − ( 2 + r ) ) 2 4 r R + 4 R − 4 r − 4 = B N " 2 = ℓ 2 = ℓ 2
Therefore, 4 r R + 4 R − 4 r − 4 = 4 R ⟹ R = r r + 1 . Now consider any point on the locus C ( x , y ) . Then x = O N = ℓ = 2 R and y = C N = R = 4 x 2 . The locus is a parabola. And the locus under the parabola is given by:
∫ a b y d x = ∫ a b 4 x 2 d x = 1 2 b 3 − a 3
where a is the value of x when 1 , r , and R are in arithmetic progression, and b is the value of x when x = y . When 1 , r , and R are in a arithmetic progression, we have:
1 + R 1 + r r + 1 2 r 2 − 2 r − 1 ⟹ r ⟹ R ⟹ a = 2 r = 2 r = 0 = 2 3 + 1 = r r + 1 = 3 + 1 3 + 3 = 3 = 2 ⋅ 3 4 1 Note that R = r r + 1 As r > 0 Since x = 2 R
Since y = 4 x 2 , when y = x ⟹ x = 4 = b . Therefore the area under the locus is
1 2 4 3 − 2 3 ⋅ 3 4 3 = 3 2 ( 2 3 − 3 4 3 )
Therefore the required answer is 2 + 3 = 5 .
Thank you for posting !
See the diagram below: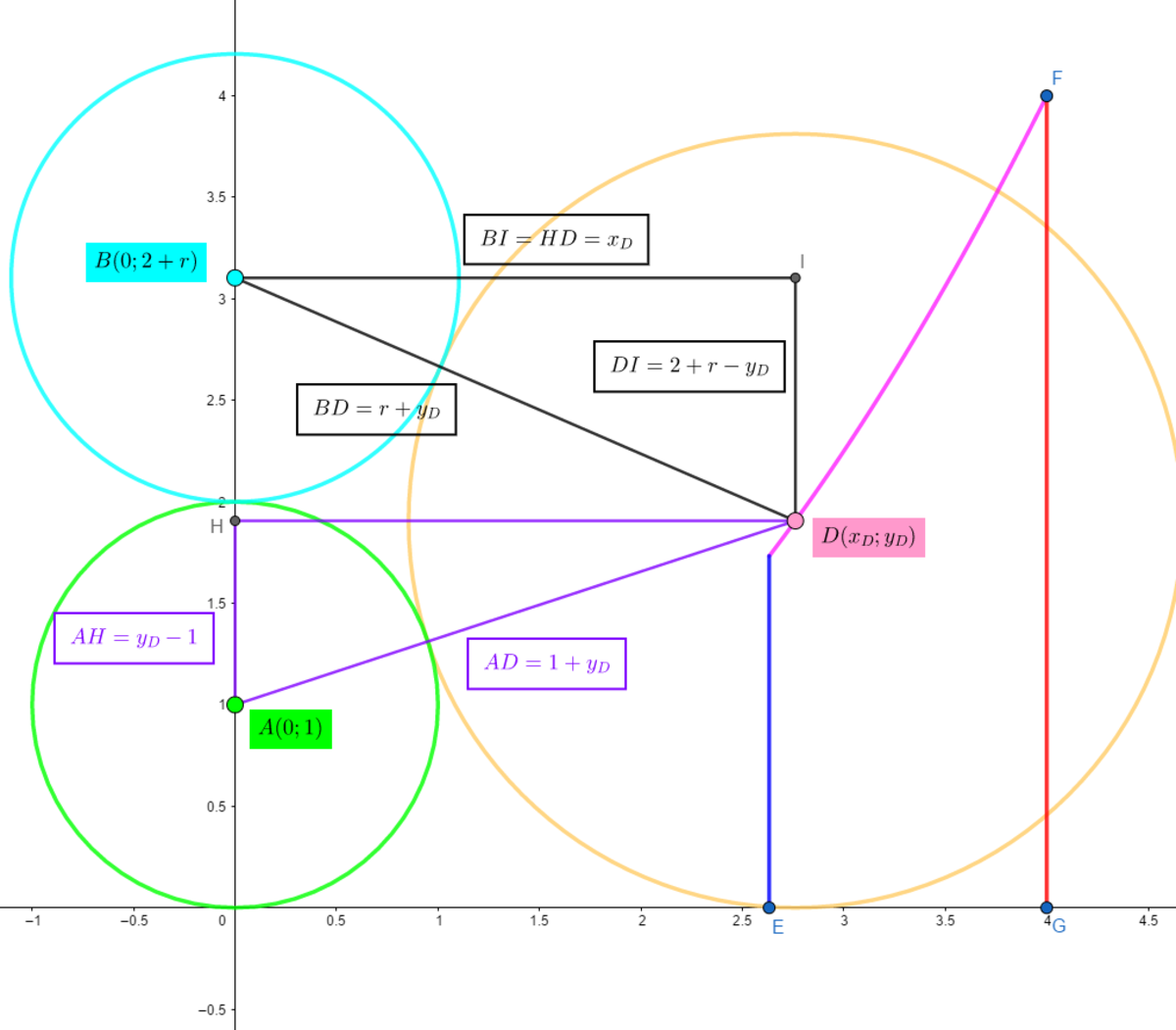 - We use the Pythagorean theorem to express
x
D
and
y
D
in terms of
r
:
- We use the Pythagorean theorem to express
x
D
and
y
D
in terms of
r
:
{ ( 1 + y D ) 2 = ( y D − 1 ) 2 + x D 2 ( r + y D ) 2 = ( 2 + r − y D ) 2 + x D 2
⎩ ⎪ ⎨ ⎪ ⎧ x D = r 2 1 + r y D = r 1 + r
Now we can express y D in terms of y D and we get the equation of the locus: y = 4 x 2
Since the radius of each circle is: 1 , r , r 1 + r . We can find the value of r for which the radii are in arithmetic progression, with 1 < r < r 1 + r . We can solve this system of equation, where k is the common difference between the radii:
⎩ ⎨ ⎧ r = 1 + k r 1 + r = r + k
⎩ ⎪ ⎨ ⎪ ⎧ k = 2 3 − 1 r = 2 3 + 1
So we can find the corresponding value of x D for r = 2 3 + 1 and we get x D = 2 ⋅ 4 3 .
Now we need to solve x D = y D . We use the equation of the locus and solve x = 4 x 2 < = > x = 4
We can evaluate the area: ∫ 2 4 3 4 4 x 2 = 3 2 ⋅ ( 8 − 3 4 3 )
So a = 2 and b = 3 , then a + b = 5