Dynamic Geometry: P41

Let r be the radius of the cyan circle, and label the diagram as follows:

Then $OA = OB - AB = 1 - r$ , so that by the Pythagorean Theorem on $\triangle OAC$ , $OC = \sqrt{OA^2 - AC^2} = \sqrt{(1 - r)^2 - r^2} = \sqrt{1 - 2r}$ .

Also from $\triangle OAC$ , $\sin \angle OAC = \cfrac{OC}{OA} = \cfrac{\sqrt{1 - 2r}}{1 - r}$ .

So the area of $\triangle ABC$ is $A_{\triangle ABC} = \cfrac{1}{2} \cdot AB \cdot AC \cdot \sin \angle BAC = \cfrac{1}{2} \cdot r \cdot r \cdot \sin \angle OAC = \cfrac{r^2\sqrt{1 - 2r}}{2(1 - r)}$ .

The maximum area will be when $\cfrac{dA_{\triangle ABC}}{dr} = \cfrac{r(3r^2 - 6r + 2)}{2\sqrt{1 - 2r}(1 - r)^2} = 0$ , which solves to $r = 1 - \cfrac{1}{\sqrt{3}}$ for $0 < r < 1$ .

The fraction of the semi-circle area colored in pink will then be $\cfrac{\frac{1}{2}\pi - \pi(1 - \frac{1}{\sqrt{3}})}{\frac{1}{2}\pi} = \cfrac{4\sqrt{3} - 5}{3}$ .

Therefore, $a = 4$ , $b = 3$ , $c = 5$ , and $a + b + c = \boxed{12}$ .

• See the diagram below:

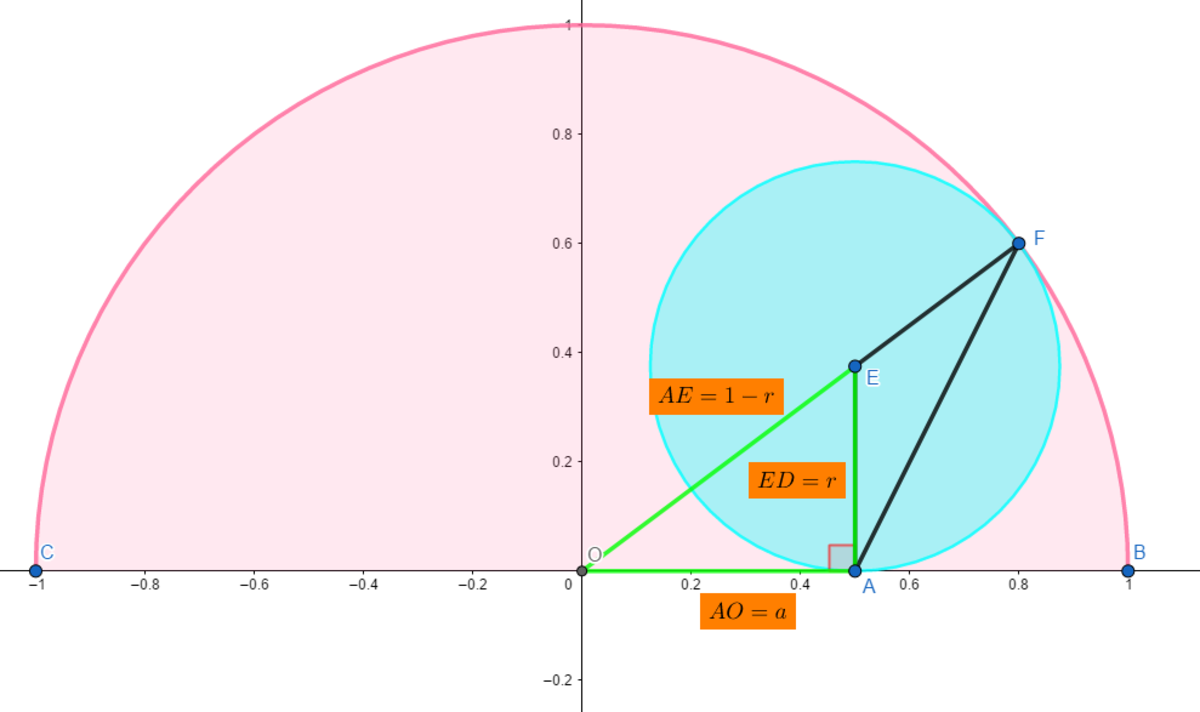
• Point $A\left(a;0\right)$ is moving on the semicircle's diameter.

• We use the Pythagorean theorem to express the radius $r$ of the cyan circle in terms of $r$ : $OE^2=EA^2+OA^2\:<=>\left(1-r\right)^2=r^2+a^2$

• We get $r=\dfrac{1}{2}\left(1-a^2\right)$

• Now we express the sinus of angle $FEA$ to get the area, basic trigonometry gives the value: $\dfrac{OA}{OE}=\dfrac{a}{1-r}=\dfrac{2a}{1+a^2}$

• Finally the area of triangle $AEF$ is: $\dfrac{1}{2}\cdot \:AE^2\cdot \dfrac{2a}{1+a^2}=\dfrac{2a}{1+a^2}\cdot \left(\dfrac{1-a^2}{2}\right)^2\cdot \dfrac{1}{2}=\dfrac{a\left(1-a^2\right)^2}{4\left(1+a^2\right)}$

• We find the derivative of this expression and get : $\dfrac{3a^6+3a^4-7a^2+1}{4\left(1+a^2\right)^2}$

• We set the derivative equal to $0$ to find the value of $a$ for which the area of the triangle is maximum:

• $\dfrac{3a^6+3a^4-7a^2+1}{4\left(1+a^2\right)^2}=0\:<=>3a^6+3a^4-7a^2+1=0$

• We factor the expression: $\left(a+1\right)\left(a-1\right)\left(3a^4+6a^2-1\right)=0$

• The only valid value for $a$ is $\sqrt{\dfrac{2}{\sqrt{3}}-1}$

• Now we evaluate the value of $r$ when $a=\sqrt{\dfrac{2}{\sqrt{3}}-1}$ , we get $r=1\:-\:\dfrac{1}{\sqrt{3}}$

• So the area of the cyan circle will be equal to $\dfrac{2}{3}\pi \cdot \left(2-\sqrt{3}\right)$

• Then the pink area is equal to: $\dfrac{-5\pi +4\sqrt{3}\pi }{6}$

• Finally the fraction of the semicircle colored in pink is equal to $\dfrac{4\sqrt{3}-5}{3}$

• $a+b+c=4+3+5=12$

Similar solution with @David Vreken 's just more trigonometry.

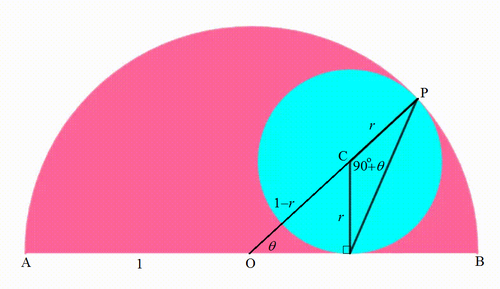
Let the diameter base and the center of the semicircle be $AB$ and $O$ and its radius $1$ . Let $C$ be the center of the semicircle and $P$ be the tangent point of the semicircle and circle at an instant. Note that $O$ , $C$ , and $P$ are colinear. At this instant let the radius of the semicircle be $r$ and $\angle POB = \theta$ . Then $\angle PCD = 90^\circ + \theta$ , where $CD$ is perpendicular to $AB$ ; and the area of $\triangle PCD$ is given by:

$\begin{aligned} A_\triangle & = \frac {r^2 \blue{\sin (90^\circ + \theta)}}2 & \small \blue{\text{Note that }\sin (180^\circ - \phi) = \sin \phi} \\ & = \frac {r^2 \blue{\cos \theta}}2 & \small \blue{\text{and }\sin (90^\circ - \phi) = \cos \phi} \\ & = \frac {r^2 \blue{\sqrt{1-2r}}}{2\blue{(1-r)}} & \small \blue{\text{Since }\sin \theta = \frac r{1-r} \implies \cos \theta = \frac {\sqrt{1-2r}}{1-r}} \end{aligned}$

To find the maximum of $A_\triangle$ ,

$\begin{aligned} \frac {dA_\triangle}{dr} & = \left(\left(2r\sqrt{1-2r} - \frac {r^2}{\sqrt{1-2r}}\right)(1-r) + r^2 \sqrt{1-2r}\right) \cdot \frac 1{2(1-r)^2} \\ & = \frac {(2r(1-2r)-r^2)(1-r)+r^2(1-2r)}{2(1-r)^2\sqrt{1-2r}} \\ & = \frac {r(3r^2-6r+2)}{2(1-r)^2\sqrt{1-2r}} \quad \quad \small \blue{\text{Putting }\frac {dA_\triangle}{dr} = 0} \\ 3r^2 - 6r + 2 & = 0 \\ \implies r & = 1 - \frac 1{\sqrt 3} \quad \quad \small \blue{\text{Since }r < 1} \end{aligned}$

Therefore $A_\triangle$ is maximum, when $r = 1 - \dfrac 1{\sqrt 3}$ , then the area of the circle $A_\bigcirc = \left(1-\dfrac 1{\sqrt 3} \right)^2 \pi = \dfrac {4-2\sqrt 3}3 \pi$ and the fraction of semicircle is pink is $\dfrac {\frac \pi 2 - \frac {4-2\sqrt 3}3}{\frac \pi 2} = \dfrac {4\sqrt 3 - 5}3$ . And the required answer is $\boxed{12}$ .