Dynamic Geometry: P46

Label the diagram as follows:

Let $a = BC$ . By Thales's Theorem $\angle ACB = 90°$ , and by the Pythagorean Theorem, $AC = \sqrt{AB^2 - BC^2} = \sqrt{2^2 - a^2} = \sqrt{4 - a^2}$ .

The inradius of the right $\triangle ABC$ is $r = \frac{1}{2}(BC + AC - AB) = \frac{1}{2}(a + \sqrt{4 - a^2} - 2)$ , which rearranges to $a = -\sqrt{-r^2 - 2r + 1} + r + 1$ .

Since $DB = FB = CB - CF = a - r$ , $OD = OB - DB = 1 - (a - r) = 1 - (-\sqrt{-r^2 - 2r + 1} + r + 1 - r) = \sqrt{-r^2 - 2r + 1}$ .

The pink curve can be defined by $x = OD = \sqrt{-r^2 - 2r + 1}$ and $y = DE = r$ , which combines and rearranges to $x^2 + (y - 1)^2 = 2$ , a circle with a center of $(0, -1)$ and a radius of $\sqrt{2}$ that intersects the black semi-circle with a central angle of $90°$ .

The area bounded by the pink curve and the black semicircle's diameter is then $A_p = \frac{90°}{360°} \pi (\sqrt{2})^2 - \frac{1}{2}(\sqrt{2})^2 \sin 90° = \frac{1}{2}\pi - 1$ .

When the sides of the cyan triangle are in arithmetic progression, $BC + AB = 2AC$ , so $a + 2 = 2\sqrt{4 - a^2}$ , which solves to $a = \frac{6}{5}$ for $a > 0$ .

At $a = \frac{6}{5}$ , $r = \frac{1}{2}(a + \sqrt{4 - a^2} - 2) = \frac{1}{2}(\frac{6}{5} + \sqrt{4 - (\frac{6}{5})^2} - 2) = \frac{2}{5}$ , so the incircle has an area of $A_c = \pi r^2 = \pi (\frac{2}{5})^2 = \frac{4}{25}\pi$ .

The ratio is then $\cfrac{A_c}{A_p} = \cfrac{\frac{4}{25}\pi}{\frac{1}{2}\pi - 1} = \cfrac{8 \cdot \pi}{25(\pi - 2)}$ , so $m = 8$ , $n = 25$ , $l = 2$ , and $m + n + l = \boxed{35}$ .

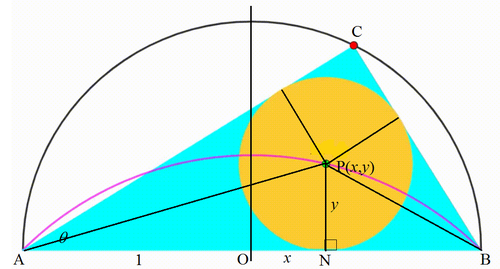
Let the center of the semicircle be $O(x,y)$ , the origin of the $xy$ -plane, a point on the locus be $P(x,y)$ , $PN$ be perpendicular to $AB$ , then $PN=y$ , the radius of the circle, and $ON = x$ , the triangle be $ABC$ , where $AB$ is the diameter of the semicircle, $\angle CAB = \theta$ , by Thale's theorem (something I learned from @David Vreken ), $\angle ACB = 90^\circ$ , and $\angle CBA = 90^\circ - \theta$ . Note that $AP$ bisects $\angle CAB$ . From

$\begin{aligned} AN + NB & = AB \\ y \cot \frac \theta 2 + y \cot \left(45^\circ - \frac \theta 2\right) & = 2 & \small \blue{\text{Note that }\frac {PN}{AN} = \frac y{1+x} = \tan \frac \theta 2} \\ 1 + x + y \cdot \frac {1+\frac y{1+x}}{1-\frac y{1+x}} & = 2 \\ 1+x + \frac {1+x+y}{1+x-y} \cdot y & = 2 \\ (1+x)^2 - y(1+x) + y(1+x) + y^2 & = 2+2x - 2y \\ x^2 + (y+1)^2 & = 2 \end{aligned}$

Therefore the locus is part of a circle with center at $(0,-1)$ and radius $\sqrt 2$ . The area under the locus is a $90^\circ$ circular segment of radius $\sqrt 2$ , $A_\ell = \dfrac \pi 4 - 1$ .

When the side lengths of $\triangle ABC$ are in a arithmetic progression, it is a $3:4:5$ or $\dfrac 65:\dfrac 85:2$ right triangle, then its inradius $y = \dfrac \Delta s = \dfrac {\frac 65 \cdot \frac 85}{\frac 65+\frac 85 + 2} = \dfrac 25$ . where $\Delta$ and $s$ are the area and semiperimeter of $\triangle ABC$ . Then the ratio of areas:

$\frac {A_\bigcirc}{A_\ell} = \frac {\frac 4{25}\pi}{\frac \pi 2-1} = \frac {8\pi}{25(\pi - 2)}$

Therefore $m+n+l = 8 + 25 + 2 = \boxed{35}$ .