Dynamic Geometry: P50

Observe, $\angle ADC=\angle BDC=\angle ACB=90^{\circ}\;\; \text{and} \;\; \angle DAC=\angle DCB$ $\begin{aligned} \implies \triangle ADC&\sim \triangle CDB \\ \frac{AD}{CD}&=\frac{CD}{BD} \\ CD^2&=AD\cdot BD \\ CD&=\sqrt{2x-x^2} \end{aligned}$ By the Pythagorean Theorem in $\triangle ADC$ and $\triangle CDB$ , $\begin{aligned} AC^2&=CD^2+AD^2 \\ AC^2&=2x-x^2+x^2 \\ \implies AC&=\sqrt{2x} \\ \\ BC^2&=CD^2+BD^2 \\ BC^2&=2x-x^2+(2-x)^2 \\ \implies BC&=\sqrt{4-2x} \end{aligned}$ Since the circle centered at $O_1$ is the incircle of $\triangle ADC$ , $\begin{aligned} \;\;\;\;\;\;\;\;\;\;\;\;20k&=\frac{AD\cdot CD}{AD+CD+AC} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; {\color{#3D99F6}r=\frac{\Delta}{s}} \\ &=\frac{x\sqrt{2x-x^2}}{x+\sqrt{2x-x^2}+\sqrt{2x}} \end{aligned}$ Since the circle centered at $O_2$ is the incircle of $\triangle CDB$ , $\begin{aligned} \;\;\;\;\;\;\;\;\;\;\;\;21k&=\frac{BD\cdot CD}{BD+CD+BC} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; {\color{#3D99F6}r=\frac{\Delta}{s}} \\ &=\frac{(2-x)\sqrt{2x-x^2}}{2-x+\sqrt{2x-x^2}+\sqrt{4-2x}} \end{aligned}$ Solving the pair of equations, $\begin{cases} 20k=\dfrac{x\sqrt{2x-x^2}}{x+\sqrt{2x-x^2}+\sqrt{2x}} \\ \\ 21k=\dfrac{(2-x)\sqrt{2x-x^2}}{2-x+\sqrt{2x-x^2}+\sqrt{4-2x}} \end{cases}$ we have, $k=\dfrac{12}{841}\implies 20k+21k=\dfrac{492}{841}$

Therefore, $p=492,\; q=841\implies p+q=\boxed{1333}$

Label the diagram as follows:

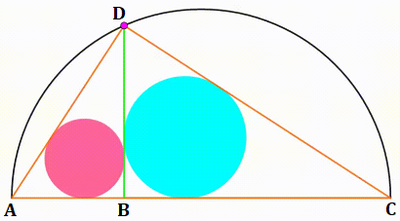
By Thales's Theorem , $\angle ADC$ is a right angle, and since $\angle ABD$ and $\angle CBD$ are also right angles, $\angle ABD = 90° - \angle ADB = \angle BDC$ , so $\triangle ADC \sim \triangle ABD \sim \triangle DBC$ by AA similarity.

Let $a = AD$ and $b = DC$ . By the Pythagorean Theorem on $\triangle ADC$ , $a^2 + b^2 = 4$ .

When the ratio of the inradii of $\triangle ABD$ and $\triangle DBC$ is $\cfrac{20}{21}$ , the ratio of the hypotenuses of $\triangle ABD$ and $\triangle DBC$ will also be $\cfrac{20}{21}$ , so $\cfrac{a}{b} = \cfrac{20}{21}$ .

The two equations $a^2 + b^2 = 4$ and $\cfrac{a}{b} = \cfrac{20}{21}$ solve to $a = AD = \cfrac{40}{29}$ and $b = DC = \cfrac{42}{29}$ .

Since $\triangle ABD \sim \triangle ADC$ , $AB = AD \cdot \cfrac{AD}{AC} = \cfrac{40}{29} \cdot \cfrac{\frac{40}{29}}{2} = \cfrac{800}{841}$ and $BD = AD \cdot \cfrac{DC}{AC} = \cfrac{40}{29} \cdot \cfrac{\frac{42}{29}}{2} = \cfrac{840}{841}$ .

The inradius of $\triangle ABD$ is then $r_1 = \cfrac{1}{2}(AB + BD - AD) = \cfrac{1}{2}\bigg(\cfrac{800}{841} + \cfrac{840}{841} - \cfrac{40}{29}\bigg) = \cfrac{240}{841}$ .

And the inradius of $\triangle BDC$ is then $r_2 = \cfrac{21}{20}r_1 = \cfrac{252}{841}$ .

Which makes the sum of the two radii $r_1 + r_2 = \cfrac{240}{841} + \cfrac{252}{841} = \cfrac{492}{841}$ , so $p = 492$ , $q = 841$ , and $p + q = \boxed{1333}$ .

The half-angle tangent substitution makes it straight forward in solving incircle problems as illustrated in this solution.

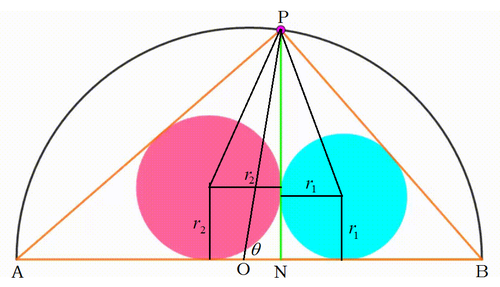
Let the center of the semicircle be $O$ , its diameter be $AB$ , the red point on the arc be $P$ , and the green segment be $PN$ . Note that $PN$ is perpendicular to $AB$ . Let $\angle POB = \theta$ , then $\angle PAB = \dfrac \theta 2$ . Due to similar triangles $\angle BPN = \dfrac \theta 2$ . Let also the radius of the cyan circle be $r_1$ . Note that the line joining $P$ and the center of the cyan circle bisect $\angle BPN$ . Therefore we have:

$\begin{aligned} r_1 \cot \frac \theta 4 + r_1 & = PN & \small \blue{\text{Let }t = \tan \frac \theta 4} \\ r_1 \cdot \frac {1+t}t & = PN & ...(1) \end{aligned}$

Similarly, let the radius of the pink circle be $r_2$ . Note that $\angle APB = 90^\circ$ . Then

$\begin{aligned} r_2 \cot \left(\frac {90^\circ - \frac \theta 2}2 \right) + r_2 & = PN \\ r_2 \cot \left(45^\circ - \frac \theta 4 \right) + r_2 & = PN \\ r_2 \cdot \frac {1+t}{1-t} + r_2 & = PN \\ r_2 \cdot \frac 2{1-t} & = PN & ...(2) \end{aligned}$

From $\dfrac {(1)}{(2)}:$

$\begin{aligned} \frac {r_1 \cdot \frac {1+t}t}{r_2 \cdot \frac 2{1-t}} & = \frac {PN}{PN} = 1 & \small \blue{\text{Putting }\frac {r_1}{r_2} = \frac {20}{21}} \\ 20 \cdot \frac {1+t}t & = 21 \cdot \frac 2{1-t} \\ 20(1-t^2) & = 42 t \\ 10t^2 + 21 t - 10 & = 0 \\ (5t-2)(2t+5) & = 0 \\ \implies t & = \frac 25 & \small \blue{\text{Since }\frac \theta 4 \text{ is acute.}} \end{aligned}$

Note that $PN = \sin \theta$ and that $\tan \dfrac \theta 2 = \dfrac {2t}{1-t^2} = \dfrac {20}{21}$ , $\tan \theta = \dfrac {2 \cdot \frac {20}{21}}{1-\left(\frac {20}{21}\right)^2} = \dfrac {840}{41}$ ., and $\sin \theta = \dfrac {840}{\sqrt{840^2+41^2}} = \dfrac {840}{841}$ . Then from $(2)$ ,

$\begin{aligned} \frac {2r_2}{1-t} & = PN = \sin \theta = \frac {840}{841} \\ \implies r_2 & = \frac {420 \left(1-\frac 25\right)}{841} = \frac {252}{841} \\ r_1 & = \frac {20}{21}r_2 \\ \implies r_1 + r_2 & = \left(\frac {20}{21} + 1 \right) r_2 = \frac {41}{21} \cdot \frac {252}{841} = \frac {492}{841} \end{aligned}$

Therefore $p+q = 492 + 841 = \boxed{1333}$ .