Dynamic Geometry: P54

Need to know :

For a triangle with side length $a,b,c\space Area=rs$ where $r$ is the radius of it's incircle and $s=\dfrac{a+b+c}{2}..........[A]$

Let the diameter of the semicircle be $\overline{AB}$ , its center point be $O$ and the other radius separating the two circle be $\overline{OP}$

Let $a=\overline{AP}, b=\overline{PB}$ and let the radius of the triangles formed be $r_1,r_2$

From Apollonius theorem we get : $a^2+b^2=4..........[1]$ Using $[A]$ relation we get : $\dfrac{ab}{2}=r_1(\frac{a}{2}+1)=r_2(\frac{b}{2}+1)$ $\Rightarrow \dfrac{r_1}{r_2}=\dfrac{\frac{b}{2}+1}{\frac{a}{2}+1}$ $=\dfrac{b+2}{a+2}=\dfrac{25}{32}$ $\Rightarrow 25a-32b=14$ $\Rightarrow a=\dfrac{14+32b}{25}..........[2]$ Putting this in $[1]$ and simplifying we get $1649b^2+896b-2304=0$ Using Quadratic formula and the inequality : $b>0$ we get $b=\dfrac{16}{17}$ Putting this in $[2]$ $a=\dfrac{30}{17}$ Now in $\triangle OPA$ and $\triangle OPB$ we know all the sides

Hence we can find that : $ar(\triangle OPA)=\dfrac{120}{289}$ $ar(\triangle OPB)=\dfrac{120}{289}$ And we can also find the semiperimeters which are $\dfrac{32}{17},\dfrac{25}{17}$ respectively

Hence using $[A]$ we can find $r_1=\dfrac{15}{68}$ $r_2=\dfrac{24}{85}$ $\Rightarrow r_1+r_2=\dfrac{171}{340}$ $\therefore Ans=171+340=\boxed{511}$

Note :

• $ar(X)$ represents area of planar figure $X$

Draw the perpendicular bisectors of the legs of the triangle, and label the diagram as follows:

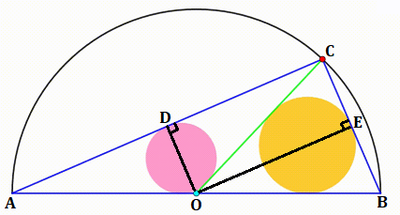
Let $x = CD$ . Then by the Pythagorean Theorem on $\triangle ODC$ , $OD = \sqrt{OC^2 - CD^2} = \sqrt{1 - x^2}$ , so the area of $\triangle AOC$ is $A_{\triangle AOC} = \frac{1}{2} \cdot AC \cdot OD = \frac{1}{2} \cdot 2x \cdot \sqrt{1 - x^2} = x\sqrt{1 - x^2}$ and the perimeter of $\triangle AOC$ is $P_{\triangle AOC} = AC + AO + OC = 2x + 1 + 1 = 2x + 2$ .

By Thales's Theorem , $\angle ACB$ is a right angle, so $ODCE$ is a rectangle, and $OE = DC = x$ and $EC = OD = \sqrt{1 - x^2}$ , which makes the area of $\triangle BOC$ $A_{\triangle BOC} = \frac{1}{2} \cdot CB \cdot OE = \frac{1}{2} \cdot 2\sqrt{1 - x^2} \cdot x = x\sqrt{1 - x^2}$ and the perimeter $P_{\triangle BOC} = CB + OB + OC = 2\sqrt{1 - x^2} + 1 + 1 = 2\sqrt{1 - x^2} + 2$ .

The inradius of $\triangle AOC$ is then $r_{\triangle AOC} = \cfrac{2A_{\triangle AOC}}{P_{\triangle AOC}} = \cfrac{2x\sqrt{1 - x^2}}{2x + 2} = \cfrac{x\sqrt{1 - x^2}}{x + 1}$ and the inradius of $\triangle BOC$ is $r_{\triangle BOC} = \cfrac{2A_{\triangle BOC}}{P_{\triangle BOC}} = \cfrac{x\sqrt{1 - x^2}}{\sqrt{1 - x^2} + 1}$ .

If the ratio of the radii is $\cfrac{25}{32}$ , then $\cfrac{r_{\triangle BOC}}{r_{\triangle AOC}} = \cfrac{\frac{x\sqrt{1 - x^2}}{\sqrt{1 - x^2} + 1}}{\frac{x\sqrt{1 - x^2}}{x + 1}} = \cfrac{x + 1}{\sqrt{1 - x^2} + 1} = \cfrac{25}{32}$ , which solves to $x = \cfrac{8}{17}$ .

Then $r_{\triangle AOC} = \cfrac{x\sqrt{1 - x^2}}{x + 1} = \cfrac{\frac{8}{17}\sqrt{1 - (\frac{8}{17})^2}}{\frac{8}{17} + 1} = \cfrac{24}{85}$ and $r_{\triangle BOC} = \cfrac{x\sqrt{1 - x^2}}{\sqrt{1 - x^2} + 1} = \cfrac{\frac{8}{17}\sqrt{1 - (\frac{8}{17})^2}}{\sqrt{1 - (\frac{8}{17})^2} + 1} = \cfrac{15}{68}$ , so $r_{\triangle AOC} + r_{\triangle BOC} = \cfrac{24}{85} + \cfrac{15}{68} = \cfrac{171}{340}$ , which means $p = 171$ , $q = 340$ , and $p + q = \boxed{511}$ .

Application of half-angle tangent substitution reduces incircles in triangle problem into solving polynomial of $t$ as shown in this solution.

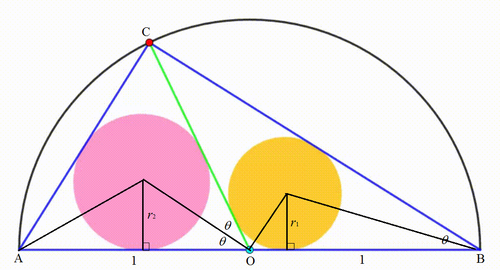
Label the center of the semicircle $O$ and the triangle $ABC$ with $AB$ being the diameter of the semicircle. Let the radii of the right and left circles be $r_1$ and $r_2$ respectively, and $\angle CBO = \theta$ , then $\angle COB = 180^\circ - 2\theta$ , $\angle COA = 2 \theta$ , and $\angle CAO = 90^\circ - \theta$ .

Consider the segment $OB$ ; we note that:

$\begin{aligned} r_1 \cot \frac {\angle COB}2 + r_1 \cot \frac {\angle CBO}2 & = OB \\ r_1 \cot \left(90^\circ - \theta\right) + r_1 \cot \frac \theta 2 & = 1 & \small \blue{\text{Let }t = \tan \frac \theta 2} \\ r_1 \cdot \frac {2t}{1-t^2} + \frac {r_1}t & = 1 \\ r_1 \cdot \frac {1+t^2}{t(1-t^2)} & = 1 & ...(1) \end{aligned}$

Similarly,

$\begin{aligned} r_2 \cot \left(45^\circ - \frac \theta 2\right) + r_2 \cot \theta & = AO \\ r_2 \cdot \frac {1+t}{1-t} + r_2 \cdot \frac {1-t^2}{2t} & = 1 \\ r_2 \cdot \frac {t^3+t^2+t+1}{2t(1-t)} & = 1 & ...(2) \end{aligned}$

From $\dfrac {(1)}{(2)}$ :

$\begin{aligned} \frac {r_1(1+t^2)\cdot 2t(1-t)}{r_2t(1-t^2)(t^3+t^2+t+1)} & = 1 \\ \frac {2r_1}{r_2(1+t)^2} & = 1 & \small \blue{\text{Putting }\frac {r_1}{r_2} = \frac {25}{32}} \\ \frac {25}{16(1+t)^2} & = 1 \\ (1+t)^2 & = \frac {25}{16} \\ 1 + t & = \frac 54 \\ \implies t & = \frac 14 \end{aligned}$

From $(1)$ : $r_1 = \dfrac {t(1-t^2)}{1+t^2} = \dfrac {15}{68}$ . The sum of two radii $r_1 + r_2 = \left(1 + \dfrac {32}{25}\right) r_1 = \dfrac {57}{25} \cdot \dfrac {15}{68} = \dfrac {171}{340}$ . Therefore $p+q = 171 + 340 = \boxed{551}$ .