Dynamic Geometry: P55
 The diagram shows a black semicircle with radius
1
. A red point is moving along its arc. We use this point and the semicircle's diameter to draw an orange triangle with its incircle in purple. The green segment is the triangle's altitude and divides the orange triangle into two smaller triangles. We draw their respective incircles (pink and cyan). When the three radii are in arithmetic progression, the sum of the areas of the three incircles can be expressed as
q
p
π
, where
p
and
q
are coprime positive integers. Find
p
+
q
.
The diagram shows a black semicircle with radius
1
. A red point is moving along its arc. We use this point and the semicircle's diameter to draw an orange triangle with its incircle in purple. The green segment is the triangle's altitude and divides the orange triangle into two smaller triangles. We draw their respective incircles (pink and cyan). When the three radii are in arithmetic progression, the sum of the areas of the three incircles can be expressed as
q
p
π
, where
p
and
q
are coprime positive integers. Find
p
+
q
.
The answer is 33.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Indeed, very simple. Nicely done!
Much better solution from a master. Should got the clue and worked backward.
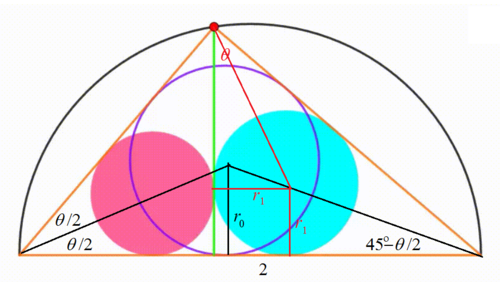
Let the radius of the largest incircle (purple) be r 0 and the left angle of the orange triangle be θ . Then the angle on the right is 9 0 ∘ − θ . And r 0 c o t 2 θ + r 0 cot ( 2 9 0 ∘ − θ ) = 2 , where 2 is the diameter of the semicircle. By half-angle tangent substitution and let t = tan 2 θ ,
t r 0 + 1 − t 1 + t r 0 t ( 1 − t ) 1 + t 2 r 0 ⟹ r 0 = 2 = 2 = 1 + t 2 2 t ( 1 − t )
Note that the length of the green segment is 2 cos θ sin θ . Let the radius of the cyan circle be r 1 . Then we have:
r 1 cot 2 θ + r 1 ( t 1 + t ) r 1 ⟹ r 1 = 2 cos θ sin θ = ( 1 + t 2 ) 2 4 t ( 1 − t 2 ) = ( 1 + t 2 ) 2 4 t 2 ( 1 − t )
Similarly, let the radius of the pink circle be r 2 . Then
r 2 cot ( 4 5 ∘ − 2 θ ) + r 2 ( 1 − t 2 ) r 2 ⟹ r 2 = 2 cos θ sin θ = ( 1 + t 2 ) 2 4 t ( 1 − t 2 ) = ( 1 + t 2 ) 2 2 t ( 1 − t 2 ) ( 1 − t )
Since r 0 > r 1 , r 2 for t > 0 , and r 1 and r 2 are interchangeable, we can assume r 1 be the middle term of the arithmetic progression. Then we have:
r 0 + r 2 1 + t 2 2 t ( 1 − t ) + ( 1 + t 2 ) 2 2 t ( 1 − t 2 ) ( 1 − t ) 1 + t 2 + 1 − t 2 ⟹ t r 0 r 1 r 2 ⟹ π r 0 2 + π r 1 2 + π r 2 2 = 2 r 1 = ( 1 + t 2 ) 2 8 t 2 ( 1 − t ) = 4 t = 2 1 = 1 + t 2 2 t ( 1 − t ) = 5 2 = ( 1 + t 2 ) 2 4 t 2 ( 1 − t ) = 2 5 8 = ( 1 + t 2 ) 2 2 t ( 1 − t 2 ) ( 1 − t ) = 2 5 6 = 6 2 5 2 0 0 π = 2 5 8 π Multiply both sides by 2 t ( 1 − t ) ( 1 + t 2 ) 2 .
Therefore a + b = 8 + 2 5 = 3 3 .
Thank you sir
Let the leg of the orange triangle on the left side be a , and the other leg be b , and let the radius of the pink incircle be r a , the radius of the cyan incircle be r b , and the radius of the purple incircle be r c .
By Thales's Theorem, the angle at the red point is right, so the orange triangles and the smaller triangles are similar to each other, which means r a = 2 a r c and r b = 2 b r c .
Since the three radii are in an arithmetic progression, r a + r c = 2 r b . Substituting r a = 2 a r c and r b = 2 b r c and solving gives a + 2 = 2 b .
By the Pythagorean Theorem on the orange triangle, a 2 + b 2 = 4 . Combining this with a + 2 = 2 b and solving gives a = 5 6 and b = 5 8 .
As an inradius of a right triangle, r c = 2 1 ( a + b − 2 ) = 2 1 ( 5 6 + 5 8 − 2 ) = 5 2 .
That means r a = 2 a r c = 2 5 6 ⋅ 5 2 = 2 5 6 and r b = 2 b r c = 2 5 8 ⋅ 5 2 = 2 5 8 .
The sum of the areas of the three incircles is S = π r a 2 + π r b 2 + π r c 2 = π ( 2 5 6 ) 2 + π ( 2 5 8 ) 2 + π ( 5 2 ) 2 = 2 5 8 π , so p = 8 , q = 2 5 , and p + q = 3 3 .