Dynamic Geometry: P61

Let the center of the big semicircle be $O$ , the radii or the cyan and green semicircle, purple and orange circles be $r_0$ , $r_1$ , $r_2$ , and $r_3$ respectively. Note that $2r_0 + 2r_1 = 2 \implies r_0 + r_1 = 1$ .

By Pythagorean theorem , we have:

$\begin{aligned} (r_0+r_2)^2 + (1-r_0)^2 & = (1-r_2)^2 \\ r_0^2 + 2r_0r_2 + r_2^2 + 1 - 2r_0 + r_0^2 & = 1 - 2r_2 + r_2^2 \\ 2r_0^2 + 2r_0r_2 - 2r_0 & = - 2r_2 \\ \implies r_2 & = \frac {r_0(1-r_0)}{1+r_0} & \small \blue{\text{Similarly,}} \\ r_3 & = \frac {r_1(1-r_1)}{1+r_1} \\ \therefore \frac {r_2}{r_3} & = \frac {11}{13} \\ \implies \frac {\frac {r_0(1-r_0)}{1+r_0}}{\frac {r_1(1-r_1)}{1+r_1}} & = \frac {11}{13} \\ 13 \cdot \frac {r_0(\blue 1-r_0)}{\blue 1+r_0} & = 11 \cdot \frac {r_1(\blue 1-r_1)}{\blue 1+r_1} & \small \blue{\text{Note that }1 = r_0+r_1} \\ 13 \cdot \frac {r_0r_1}{2r_0 + r_1} & = 11 \cdot \frac {r_1r_0}{r_0+2r_1} \\ \frac {13}{2r_0 + r_1} & = \frac {11}{r_0+2r_1} \\ 13r_0 + 26r_1 & = 22r_0 + 11r_1 \\ 15r_1 & = 9r_0 \\ \implies \frac {r_0}{r_1} & = \frac 53 \end{aligned}$

Therefore $p+q = 5+3 = \boxed 8$ .

Let the black semicircle have a radius of $1$ , let the $r_p$ be the radius of the purple circle, $r_o$ be the radius of the orange circle, $r_c$ be the radius of the cyan semicircle, and $r_g$ be the radius of the green semicircle, and label the diagram as follows:

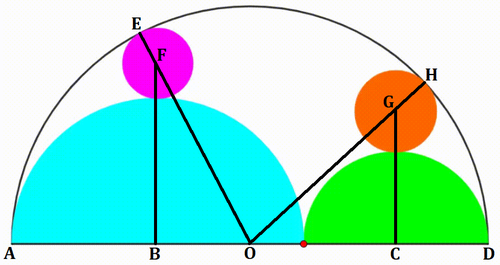
From segment $AD$ , $2r_c + 2r_g = 2$ , or $r_c + r_g = 1$ .

From the given ratio of the purple and orange circle radii, $\cfrac{r_p}{r_o} = \cfrac{11}{13}$ .

By the Pythagorean Theorem on $\triangle OBF$ , $(1 - r_c)^2 + (r_p + r_c)^2 = (1 - r_p)^2$ .

And by the Pythagorean Theorem on $\triangle OCG$ , $(1 - r_g)^2 + (r_g + r_o)^2 = (1 - r_o)^2$ .

These four equations can be solved to $r_c = \cfrac{5}{8}$ , $r_g = \cfrac{3}{8}$ , $r_p = \cfrac{15}{104}$ , and $r_o = \cfrac{15}{88}$ .

Therefore, the ratio of the cyan and green circle radii is $\cfrac{r_c}{r_g} = \cfrac{\frac{5}{8}}{\frac{3}{8}} = \cfrac{5}{3}$ , so $p = 5$ , $q = 3$ , and $p + q = \boxed{8}$ .