Dynamic Geometry: P62
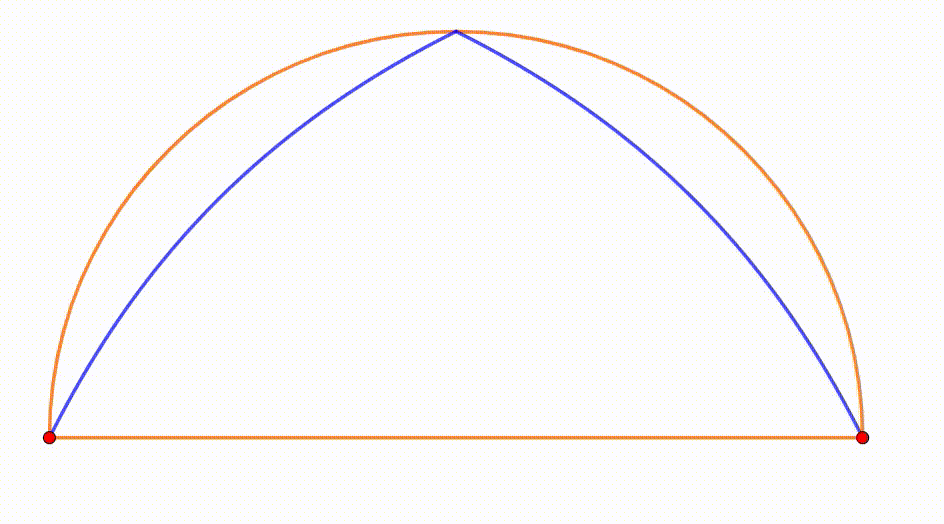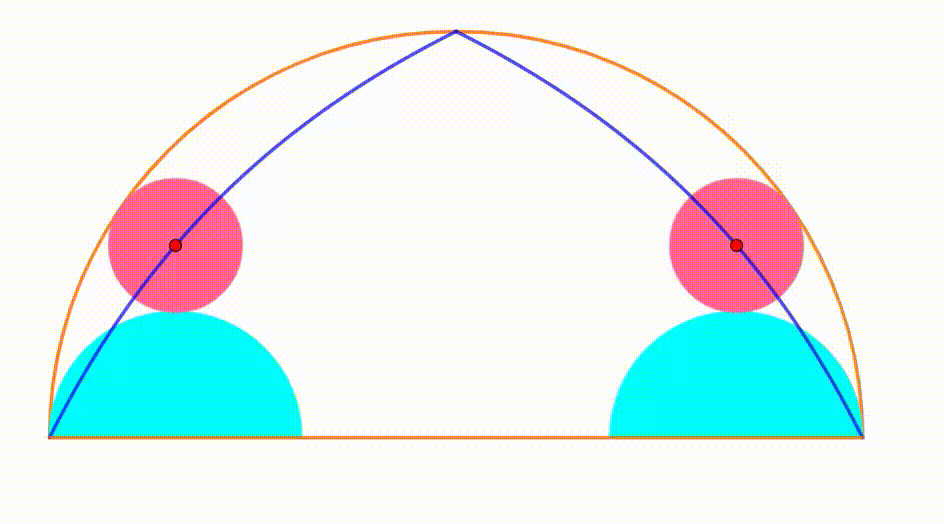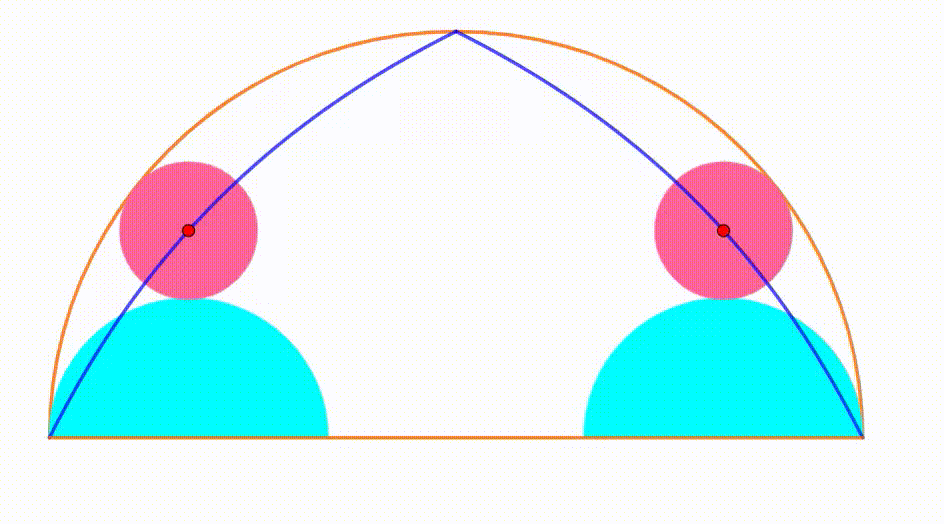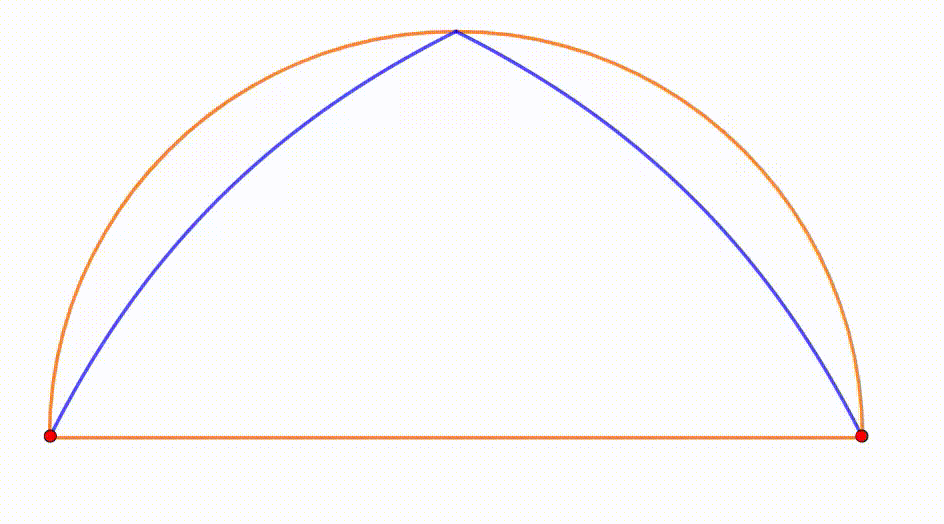 The diagram shows an orange semicircle with radius
1
. Two cyan semicircles are growing and shrinking symmetrically so they are internally tangent to the orange semicircle. Each pink circle is internally tangent to the orange semicircle and tangent to a cyan semicircle so their center shares the same
x
coordinate. The center of both pink circle traces a
locus
(blue curves). The area bounded by the blue curves and the orange semicircle's diameter can be expressed as
p
−
q
ln
(
p
)
, where
p
and
q
are positive integers. Find
p
+
q
.
The diagram shows an orange semicircle with radius
1
. Two cyan semicircles are growing and shrinking symmetrically so they are internally tangent to the orange semicircle. Each pink circle is internally tangent to the orange semicircle and tangent to a cyan semicircle so their center shares the same
x
coordinate. The center of both pink circle traces a
locus
(blue curves). The area bounded by the blue curves and the orange semicircle's diameter can be expressed as
p
−
q
ln
(
p
)
, where
p
and
q
are positive integers. Find
p
+
q
.
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Well, you are quit busy today !
Log in to reply
Actually yes. Went with wife to do shopping and sent 14 documents to my prospective customers in Vietnam today before I submitted the solutions. Although retired, I am marketing animal health products from Germany.
Holy molly !
Log in to reply
What is your mother tongue? French? Flemish? I stopped over at Brussels twice as a tourist. Nice beer and mussels.
Let the r p be the radius of the pink circle and r c be the radius of the cyan semicircle, and label the diagram as follows:
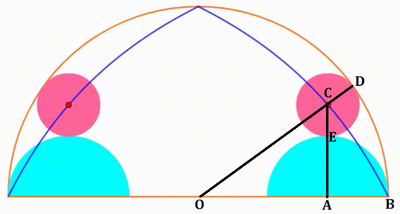
Then O A = O B − A B = 1 − r c , A C = A E + E C = r c + r p , and O C = O D − C D = 1 − r p .
The blue curve has x = O A = 1 − r c and y = A C = r c + r p , so that r c = 1 − x and r p = y − r c = y − ( 1 − x ) , which makes O C = 1 − r p = 1 − ( y − ( 1 − x ) ) = 2 − x − y .
By the Pythagorean Theorem on △ O A C , O A 2 + A C 2 = O C 2 or x 2 + y 2 = ( 2 − x − y ) 2 , which rearranges to y = 2 + x − 2 2 .
The area bounded by the blue curves and the orange semicircle's diameter is then 2 ∫ 0 1 ( 2 + x − 2 2 ) d x = 4 − 2 ln 4 , so p = 4 , q = 2 , and p + q = 6 .
Let the center of the big semicircle be O ( 0 , 0 ) , the origin of the x y -plane, an arbitrary point of the right locus as P ( x , y ) , P N be perpendicular to the x -axis, and the radii of the cyan semicircle and pink circle be r and r 1 respectively. Then we have:
{ x = O N = 1 − r y = P N = r + r 1
By Pythagorean theorem , we have:
O N 2 + P N 2 x 2 + y 2 x y − 2 x − 2 y + 2 ⟹ y = O P 2 = ( 1 − r 1 ) 2 = ( 1 − ( 1 − r + r + r 1 − 1 ) ) 2 = ( 1 − ( x + y − 1 ) ) 2 = ( 2 − x − y ) 2 = x 2 + 2 x y + y 2 − 4 ( x + y ) + 4 = 0 = 2 − x 2 ( 1 − x )
The above is the equation of the locus. The area under the two loci is
A = 2 ∫ 0 1 y d x = 2 ∫ 0 1 2 − x 2 ( 1 − x ) d x = 2 ∫ 0 1 ( 2 − 2 − x 2 ) d x = 4 x + 4 ln ( 2 − x ) ∣ ∣ ∣ ∣ 0 1 = 4 − 4 ln 2 = 4 − 2 ln 4
Therefore p + q = 4 + 2 = 6 .