Dynamic Geometry: P63
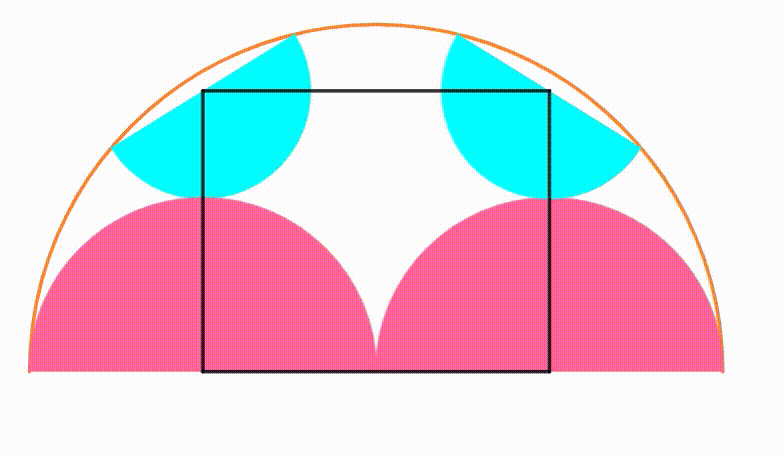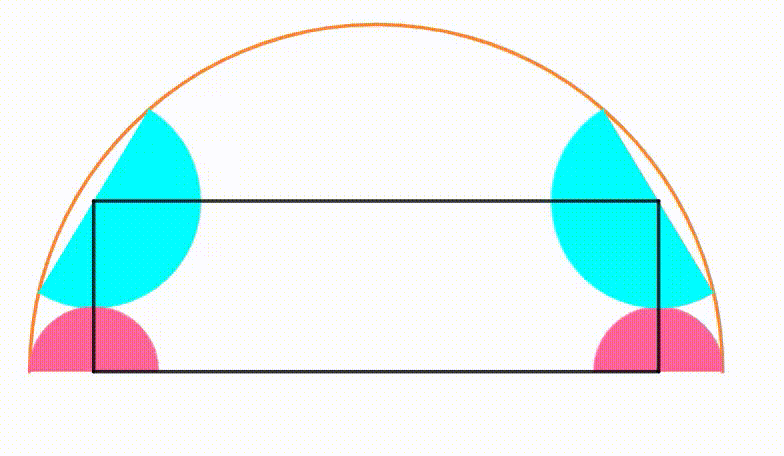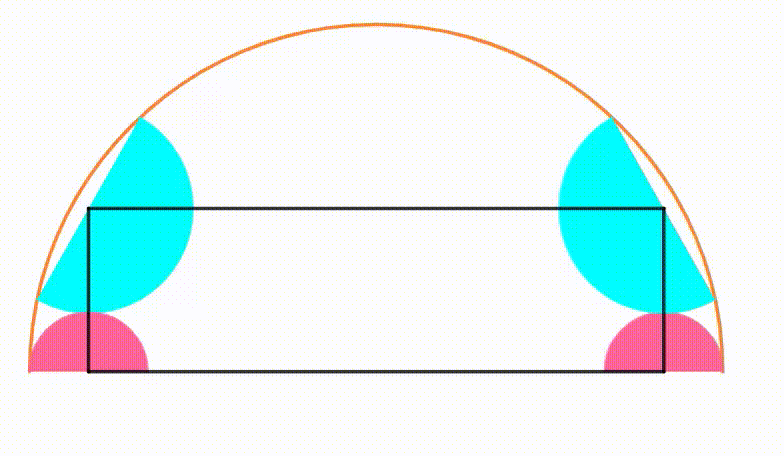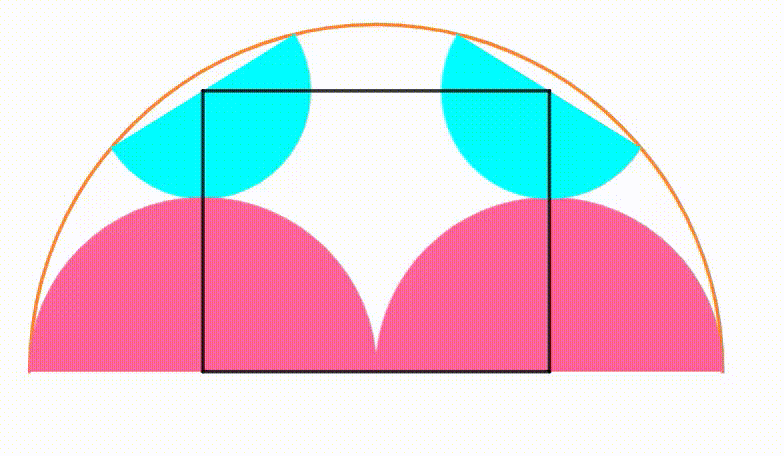 The diagram shows an orange semicircle with radius
. Two pink semicircles are growing and shrinking symmetrically so they are internally tangent to the orange semicircle. Each cyan semicircle is internally tangent to the orange semicircle and tangent to a pink semicircle so their center shares the same
coordinate. Using the four centers, we draw a black rectangle. When the area of the black rectangle is
maximum
, the ratio of its perimeter to its area can be expressed as
, where
and
are coprime positive integers. Find
.
The diagram shows an orange semicircle with radius
. Two pink semicircles are growing and shrinking symmetrically so they are internally tangent to the orange semicircle. Each cyan semicircle is internally tangent to the orange semicircle and tangent to a pink semicircle so their center shares the same
coordinate. Using the four centers, we draw a black rectangle. When the area of the black rectangle is
maximum
, the ratio of its perimeter to its area can be expressed as
, where
and
are coprime positive integers. Find
.
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the center of the big semicircle be O ( 0 , 0 ) , the radii of the pink and cyan semicircles be r 0 and r 1 respectively, and center of the right cyan semicircle be P ( k , h ) . Then k = 1 − r 0 and h = r 0 + r 1 . The equation of the big semicircle is x 2 + y 2 = 1 and that of the cyan semicircle is ( x − k ) 2 + ( y − h ) 2 = r 1 2 . The two intersection points A and B satisfy:
x 2 − 2 k x + k 2 + y 2 − 2 h y + h 2 1 − 2 k x + k 2 − 2 h y + h 2 = r 1 2 = r 1 2 Note that x 2 + y 2 = 1
This is the equation of the diameter A B of the cyan semicircle. Since the center P ( k , h ) is on A B , putting x = k and y = h , we have:
1 − 2 k 2 + k 2 − 2 h 2 + h 2 k 2 + h 2 + r 1 2 k 2 + h 2 + ( k + h − 1 ) 2 k 2 + h 2 + k 2 + 2 k h + h 2 − 2 k − 2 h + 1 k 2 + h 2 + k h − k − h ( k + h ) 2 − 2 k h + k h − ( k + h ) k h ⟹ k h ( 1 − r 0 ) ( r 0 + r 1 ) r 0 + r 1 − r 0 2 − r 0 r 1 r 1 2 + r 0 r 1 = r 1 2 = 1 = 1 = 1 = 0 = 0 = ( k + h ) 2 − ( k + h ) = ( 1 + r 1 ) 2 − 1 − r 1 = r 1 ( 1 + r 1 ) = r 1 2 + r 1 = r 1 2 + r 1 = r 0 − r 0 2 Rearranging Note that k + h = 1 + r 1 ⟹ k + h − 1 = r 1 . . . ( 1 ) . . . ( 2 )
Note that the area of the rectangle A = 2 k h . A is maximum when k h is maximum. Equation ( 1 ) : k h = r 1 ( 1 + r 1 ) shows that k h is maximum, when r 1 is maximum. From ( 2 ) :
r 1 2 + r 0 r 1 + r 0 2 − r 0 2 r 1 ⋅ d r 0 d r 1 + r 1 + r 0 ⋅ d r 0 d r 1 ⟹ r 1 = 0 = 1 − 2 r 0 = 1 − 2 r 0 Differentiate both sides w.r.t. r 0 Putting d r 0 d r 1 = 0
This means that A is maximum, when r 1 = 1 − 2 r 0 . From ( 2 ) :
( 1 − 2 r 0 ) 2 + r 0 ( 1 − 2 r 0 ) 1 − 4 r 0 + 4 r 0 2 + r 0 − 2 r 0 2 3 r 0 2 − 4 r 0 + 1 ( 3 r 0 − 1 ) ( r 0 − 1 ) = r 0 − r 0 2 = r 0 − r 0 2 = 0 = 0
This means that when r 0 = 3 1 and r 1 = 1 − 2 r 0 = 3 1 , A = 2 k h = 2 r 1 ( 1 + r 1 ) = 9 8 is maximum (when r 0 = 1 , r 1 = − 1 which is not acceptable). Then the perimeter of the rectangle p = 4 ( 1 − r 0 ) + 2 ( r 0 + r 1 ) = 4 . Then A p = 9 8 4 = 2 9 and p + q = 9 + 2 = 1 1 .