Dynamic Geometry: P64
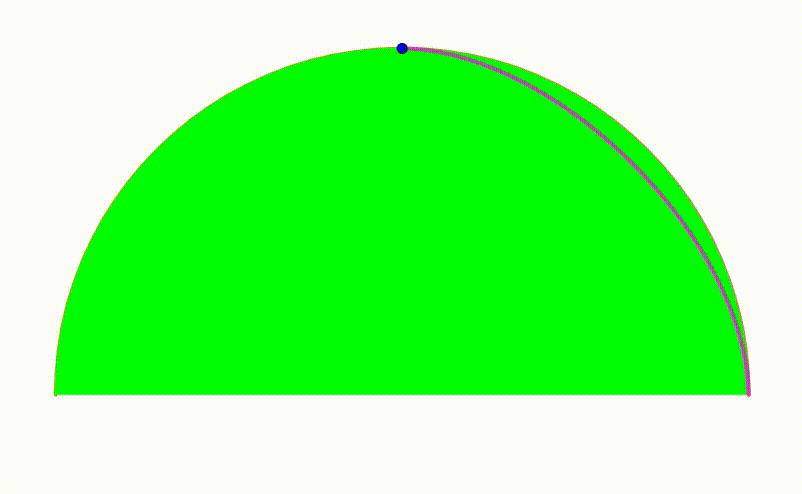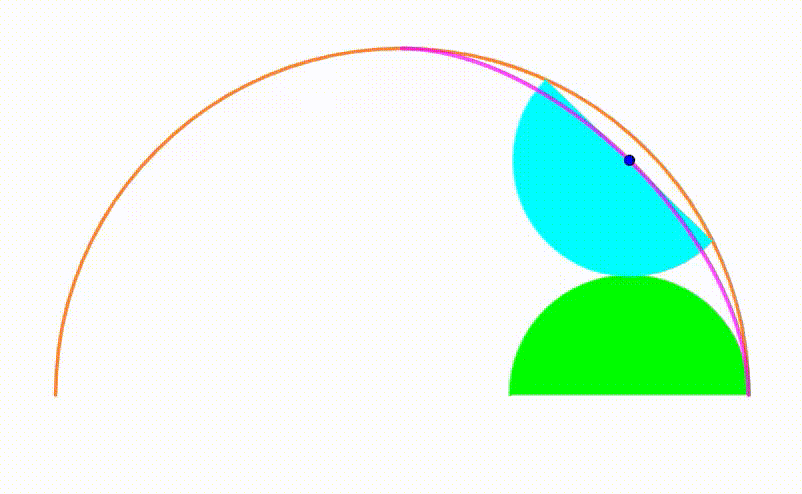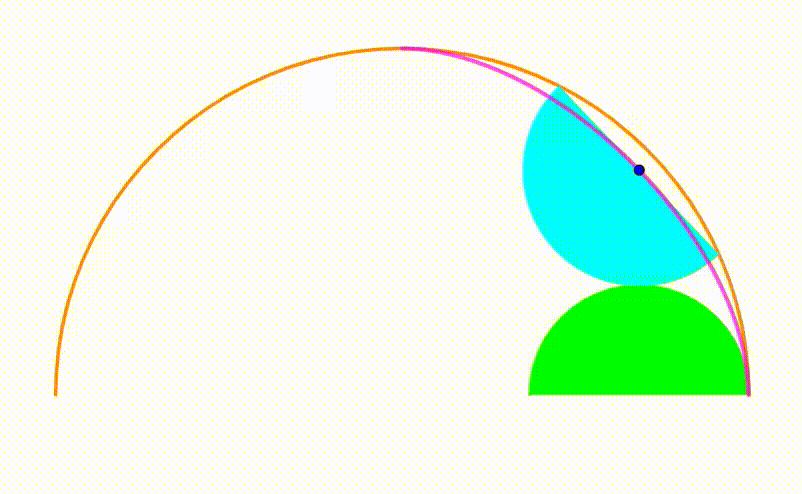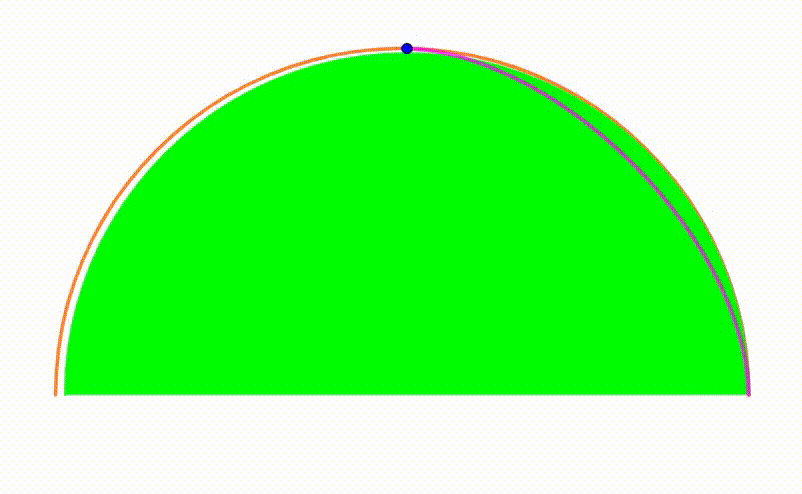 The diagram shows an orange semicircle with radius
. A green semicircle grows and shrinks so its internally tangent to the orange semicircle. The cyan semicircle is internally tangent to the orange semicircle and tangent to the green semicircle so their center shares the same
coordinate. The center of the cyan semicircle traces a
locus
(pink curve). The area bounded by the pink curve and its tangent circular arc can be expressed as:
The diagram shows an orange semicircle with radius
. A green semicircle grows and shrinks so its internally tangent to the orange semicircle. The cyan semicircle is internally tangent to the orange semicircle and tangent to the green semicircle so their center shares the same
coordinate. The center of the cyan semicircle traces a
locus
(pink curve). The area bounded by the pink curve and its tangent circular arc can be expressed as:
where and are coprime positive integers and is square-free. Find .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The locus of the center of the cyan semicircle is part of an ellipse. This solution proves it.
Let the center of the big semicircle be O ( 0 , 0 ) , the origin of the x y -plane. Tilt the figure by 4 5 ∘ counterclockwise. Let the center and radius of the cyan semicircle be P ( k , h ) and r 1 , and those of the green semicircle Q and r 0 .
Then Q = ( 2 1 − r 0 , 2 1 − r 0 ) . Note that P Q = r 0 + r 1 . Therefore the coordinates of P are
⎩ ⎪ ⎨ ⎪ ⎧ k = 2 1 − 2 r 0 − r 1 h = 2 1 + r 1
The equation of the cyan semicircle is ( x − k ) 2 + ( y − h ) 2 = r 1 2 and that of the big semicircle is x 2 + y 2 = 1 . The two points of intersection satisfy both equations and we have:
1 − 2 k x + k 2 − 2 h y + h 2 = r 1 2
which is the diameter of the cyan semicircle. Since the center P ( k , h ) is on the diameter, putting x = k and y = h ,
1 − 2 k 2 + k 2 − 2 h 2 + h 2 k 2 + h 2 + r 1 2 k 2 + h 2 + ( 2 h − 1 ) 2 k 2 + 3 h 2 − 2 2 h k 2 + 3 ( h − 3 2 ) 2 3 2 k 2 + 9 2 ( h − 3 2 ) 2 3 2 x 2 + 9 2 ( y − 3 2 ) 2 = r 1 2 = 1 = 1 = 0 = 3 2 = 1 = 1 Since h = 2 1 + r 1 2 Replace k with x and h with y .
Therefore, the locus is part of an ellipse with center at C ( 0 , 3 2 ) , major-axis of a = 3 2 and minor-axis of b = 3 2 . Solving the ellipse equation with x 2 + y 2 = 1 , we can find the two tangent points of the ellipse and the big semicircle are A ( − 2 1 , 2 1 ) and B ( 2 1 , 2 1 ) . The area bounded by the semicircle and the ellipse is given by:
A = 9 0 ∘ circular segment − 1 2 0 ∘ elliptical segment = 4 π − 2 1 − a b ( 3 π a 2 − 2 1 a 2 sin 1 2 0 ∘ ) = 4 π − 2 1 − a b ( 3 π − 4 3 ) = 4 π − 2 1 − 3 3 2 ( 3 π − 4 3 ) = 4 π − 3 1 − 9 3 2 π
Therefore the required answer is 4 + 3 = 7 .