Dynamic Geometry: P69
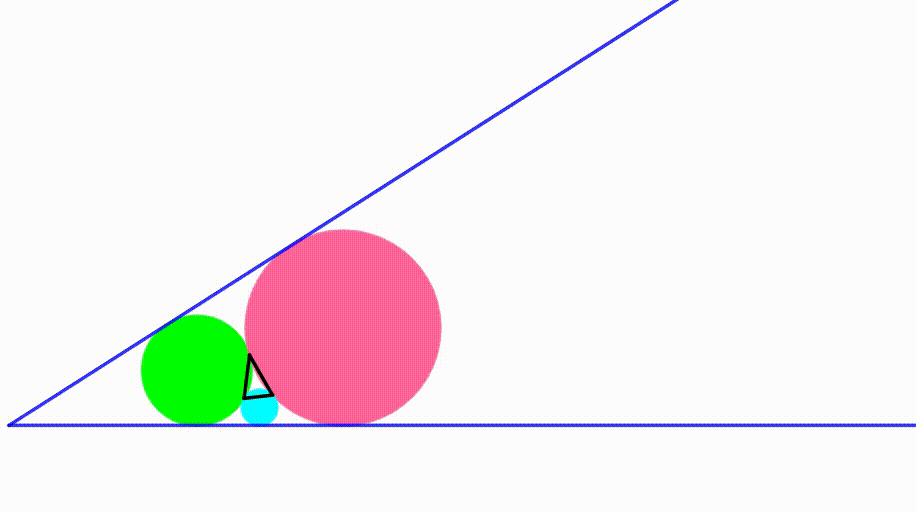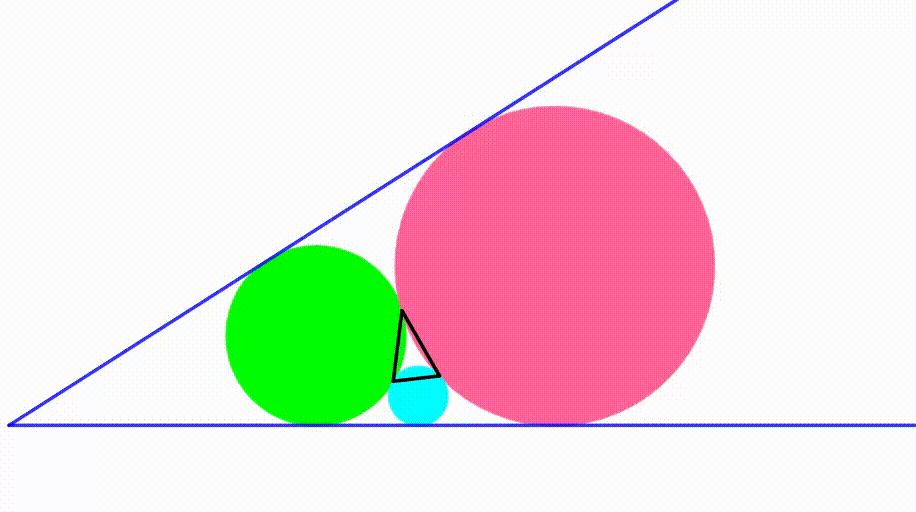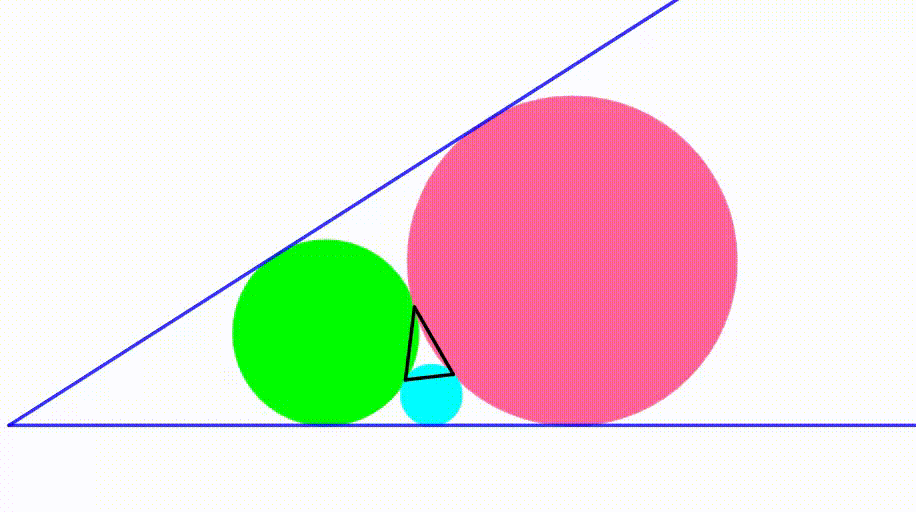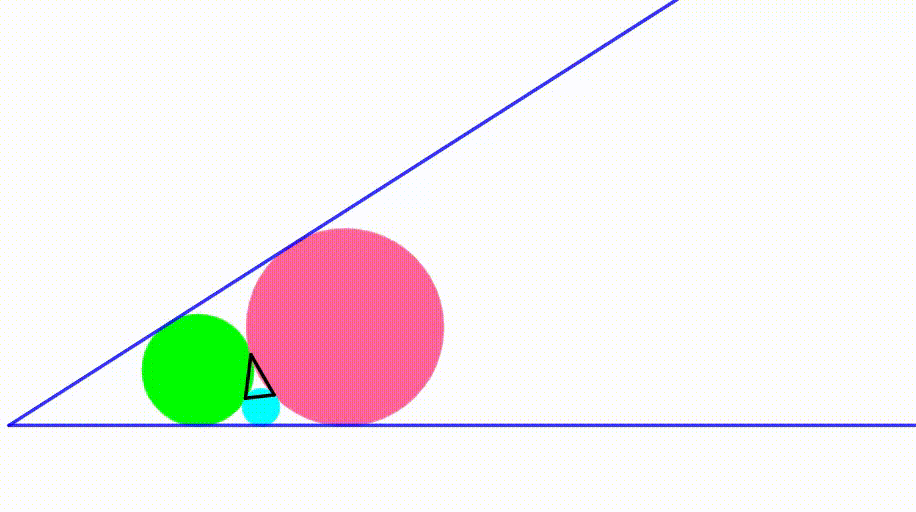 The diagram shows a blue angle which measures
tan
−
1
(
5
2
7
3
3
6
)
. Three circles (green, cyan and red) tangent to each other and internally tangent to the angle are moving freely inside the angle. Using the tangency points between them, we draw a black triangle. When the area of the black triangle is equal to
1
6
9
6
5
1
8
1
3
, the sum of the radii of all three circles can be expressed as
q
p
, where
p
and
q
are coprime positive integers. Find
p
+
q
.
The diagram shows a blue angle which measures
tan
−
1
(
5
2
7
3
3
6
)
. Three circles (green, cyan and red) tangent to each other and internally tangent to the angle are moving freely inside the angle. Using the tangency points between them, we draw a black triangle. When the area of the black triangle is equal to
1
6
9
6
5
1
8
1
3
, the sum of the radii of all three circles can be expressed as
q
p
, where
p
and
q
are coprime positive integers. Find
p
+
q
.
The answer is 9869.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Thank you, nice one not using coordinates.
Log in to reply
You are welcome. Just put a comment on P68 like "Hi". Then I can edit your comment and post my solution there. Being a moderator has its advantages.
I have simplified the solution above. Found an formula combining the steps together.
Δ b = ( r 0 + r 1 ) ( r 1 + r 2 ) ( r 2 + r 0 ) 2 r 0 r 1 r 2 Δ
It will easier for P71, P72, and P73.
Let the angle measuring tan − 1 5 2 7 3 3 6 be ∠ P O Q = θ , the centers of the green, red, and cyan circles be A , B , and C and their radii r 0 , r 1 , and r 2 respectively, and A M and B N be perpendicular to O Q .
We note that ∠ B O N = 2 θ and tan 2 θ = sin θ 1 − cos θ = 2 4 7 . This means that similar △ A O M and △ B O N are 7 - 2 4 - 2 5 triangles. By similar triangles:
A M B N r 0 r 1 2 5 r 1 ⟹ r 1 = O A O B = O A O A + A B = 7 2 5 r 0 7 2 5 r 0 + r 0 + r 1 = 3 2 r 0 + 7 r 1 = 9 1 6 r 0
Using the equation, r 2 1 = r 0 1 + r 1 1 = r 0 1 + 4 r 0 3 ⟹ r 2 = 4 9 1 6 r 0 . By Heron's formula , the area of △ A B C , Δ = ( r 0 + r 1 + r 2 ) r 0 r 1 r 2 = 4 4 1 5 9 2 r 0 2 . Let the area of the "black" triangle be Δ b . Then
Δ b = ( r 0 + r 1 ) ( r 1 + r 2 ) ( r 2 + r 0 ) 2 r 0 r 1 r 2 Δ = 4 7 1 2 5 7 0 5 6 Δ
Putting δ = 1 6 9 6 5 1 8 1 3 , we have
4 7 1 2 5 7 0 5 6 Δ 4 7 1 2 5 7 0 5 6 ⋅ 4 4 1 5 9 2 r 0 2 ⟹ r 0 r 0 + r 1 + r 2 ⟹ p + q = 1 6 9 6 5 1 8 1 3 = 1 6 9 6 5 1 8 1 3 = 4 8 3 5 = ( 1 + 9 1 6 + 4 9 1 6 ) r 0 = 3 0 2 4 6 8 4 5 = 9 8 6 9