Dynamic Geometry: P75

Let $O$ and $P$ be the centers of the yellow and cyan semicircles, their radii $1$ and $r$ , and diameters $CD$ and $AB$ respectively, and the triangle be $OPN$ , where $OP=a$ and $ON=b$ . By intersection chords theorem ,

$\begin{aligned} AP \cdot PB & = CP \cdot PD \\ r \cdot r & = (1-a)(1+a) \\ \implies r^2 & = 1 - a^2 \end{aligned}$

By Pythagorean theorem ,

$\begin{aligned} ON^2 + PN^2 & = OP^2 \\ b^2 +r^2 & = a^2 = 1 - r^2 \\ b^2 & = 1 - 2r^2 \\ \implies b & = \sqrt{1-2r^2} \end{aligned}$

The area of $\triangle OPN$ is given by:

$\begin{aligned} A & = \frac 12 br = \frac {r\sqrt{1-2r^2}}2 & \small \blue{\text{To find maximum }A} \\ \frac {dA}{dr} & = \frac {1-4r^2}{2\sqrt{1-2r^2}} & \small \blue{\text{Putting }\frac {dA}{dr} = 0} \\ \implies r & = \frac 12 \end{aligned}$

This means that $A$ is maximum when $r= \dfrac 12$ , then

$\frac {A_{\rm cyan}}{A_{\rm yellow}} = \frac {\frac \pi 4}{\pi - \frac \pi 4} = \frac 13$

Therefore $p+q = 1+3 = \boxed 4$ .

Label the diagram as follows, where $O$ , $K$ are the radii of the yellow and cyan semicircles respectively, $L$ is the intersection of the cyan semicircle with the diameter of the yellow semicircle, $AB$ and $CD$ are the diameters of the two semicircles. For simplicity we set the radius of the yellow semicircle to be $R=1$ .

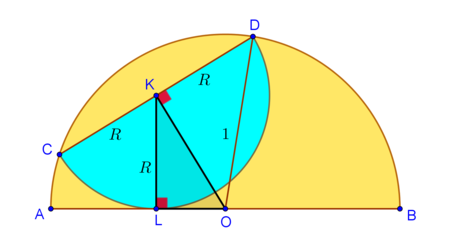By Pythagorean theorem on $\triangle OKD$ , $O{{K}^{2}}=O{{D}^{2}}-K{{D}^{2}}=1-{{R}^{2}}$ By Pythagorean theorem on $\triangle OKL$ , $O{{L}^{2}}=O{{K}^{2}}-K{{L}^{2}}=\left( 1-{{R}^{2}} \right)-{{R}^{2}}\Rightarrow OL=\sqrt{1-2{{R}^{2}}}$ Hence, $\left[ OKL \right]=\frac{1}{2}KL\cdot OL=\frac{1}{2}R\cdot \sqrt{1-2{{R}^{2}}}$ Taking the derivative of $f\left( R \right)=\frac{1}{2}R\sqrt{1-2{{R}^{2}}}$ , $R\in \left( 0,\frac{1}{\sqrt{2}} \right]$ , ${f}'\left( R \right)=\frac{1}{2}\left( \sqrt{1-2{{R}^{2}}}+R\frac{-2R}{2\sqrt{1-2{{R}^{2}}}} \right)=\frac{1}{2}\frac{1-4{{R}^{2}}}{\sqrt{1-2{{R}^{2}}}}$ Hence, ${f}'\left( R \right)=0\Leftrightarrow 1-4{{R}^{2}}=0\overset{R>0}{\mathop{\Leftrightarrow }}\,R=\frac{1}{2}\in \left( 0,\frac{1}{\sqrt{2}} \right]$ This implies that the area of the black triangle gets maximised when $R=\dfrac{1}{2}$ .

Then, $\frac{\text{Cyan area}}{\text{Yelow area}}=\frac{\frac{1}{2}\pi {{\left( \frac{1}{2} \right)}^{2}}}{\frac{1}{2}\pi {{\left( 1 \right)}^{2}}-\frac{1}{2}\pi {{\left( \frac{1}{2} \right)}^{2}}}=\frac{1}{3}$ For the answer, $p=1$ , $q=3$ , thus, $p+q=\boxed{4}$ .