Dynamic Geometry: P78
 The diagram shows a unit black square. A red quarter circle is drawn using the side of the square as the radius. Two yellow semicircles are drawn. Each center moves on one square's side so the semicircles are growing, shrinking and are tangent to each other at any moment. Then, we draw a cyan circle so it's tangent to the two yellow semicircles and internally tangent to the red quarter circle. Finally we inscribed a blue circle between the cyan circle and the two yellow semicircles. When the sum of all radii (except the red quadrant) is equal to
1
1
2
1
1
7
, the ratio of the larger semicircle's radius to the radius of the smaller semicircle can be expressed as
q
p
, where
p
and
q
are coprime positive integers. Find
p
+
q
.
The diagram shows a unit black square. A red quarter circle is drawn using the side of the square as the radius. Two yellow semicircles are drawn. Each center moves on one square's side so the semicircles are growing, shrinking and are tangent to each other at any moment. Then, we draw a cyan circle so it's tangent to the two yellow semicircles and internally tangent to the red quarter circle. Finally we inscribed a blue circle between the cyan circle and the two yellow semicircles. When the sum of all radii (except the red quadrant) is equal to
1
1
2
1
1
7
, the ratio of the larger semicircle's radius to the radius of the smaller semicircle can be expressed as
q
p
, where
p
and
q
are coprime positive integers. Find
p
+
q
.
The answer is 97.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Well, that is very detailed indeed, thanks !
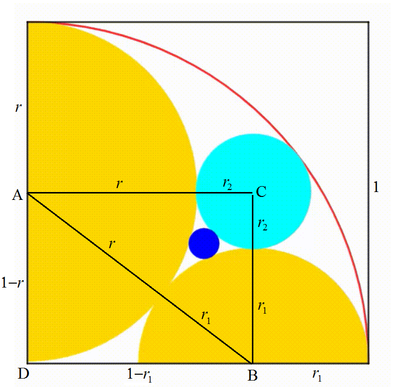
Let the centers and radii of the left semicircle, right semicircle and cyan circle be A , B , and C and r , r 1 , and r 2 respectively and the bottom-left vertex of the unit square be D . By Pythagorean theorem , we note that
A D 2 + B D 2 ( 1 − r ) 2 + ( 1 − r 1 ) 2 2 − 2 r − 2 r 1 1 − r ⟹ r 1 = A B 2 = ( r + r 1 ) 2 = 2 r r 1 = r 1 + r r 1 = 1 + r 1 − r
Also note that A C = B D ⟹ r + r 2 = 1 − r 1 ⟹ r + r 1 + r 2 = 1 ⟹ r 2 = 1 − r − r 1 = 1 + r r ( 1 − r ) = r r 1 .
Let the radius of the blue circle be r 3 . Then by Descarte's theorem ,
r 3 1 ⟹ r 3 = r 1 + r 1 1 + r 2 1 + 2 r r 1 1 + r 1 r 2 1 + r 2 r 1 = r r 1 r 2 r r 1 + r 1 r 2 + r 2 r + 2 r r 1 r 2 r + r 1 + r 2 + r = r 2 2 r 2 ( 1 + r + r 1 + 2 r 2 2 1 = r 2 1 + 1 − r 2 + r 2 2 = r 2 4 − r 2 = 4 − r 2 r 2
When the sum of all radii is 1 1 2 1 1 7 :
r + r 1 + r 2 + r 3 1 + 4 − r 2 r 2 4 − r 2 4 ⟹ r 2 ( 1 + r ) r ( 1 − r ) 1 1 7 r 2 − 9 7 r + 2 0 ( 1 3 r − 5 ) ( 9 r − 4 ) r , r 1 = 1 1 2 1 1 7 = 1 1 2 1 1 7 = 1 1 2 1 1 7 = 1 1 7 2 0 = 1 1 7 2 0 = 0 = 0 = 1 3 5 , 9 4 Since r and r 1 are interchangeable.
Then the ratio of larger radius to the other radius is 9 4 ⋅ 5 1 3 = 4 5 5 2 and p + q = 5 2 + 4 5 = 9 7 .
Thank you for posting !
Step 1: To prove that E is the center of the cyan circle.
It is easy to see that Q and R belong to the diagonal B D of the square. Moreover, Q E = K H − K Q − E H = K H − K Q − L B = 1 − r 1 − r 2 ( 1 ) Similarly, E R = I L − I E − R L = I L − D K − R L = 1 − r 1 − r 2 Hence the circle with center E and radius y = Q E = E R = 1 − r 1 − r 2 is tangent to both semicircles. Furthermore, E J = A J − A E = A J − K L = 1 − ( r 1 + r 2 ) = y Thus, E is the center of the cyan circle tangent to the semicircles and the red arc.
Step 2: To establish relations for r 1 , r 2 and r 3
From ( 1 ) we get r 1 + r 2 + r 3 = 1 ( 2 ) By Pythagorean theorem on △ A K L we have
K L 2 = A K 2 + A L 2 ⇒ ( r 1 + r 2 ) 2 = ( 1 − r 1 ) 2 + ( 1 − r 2 ) 2 which gives r 1 + r 2 = 1 − r 1 r 2 ( 3 ) The latter, combined with ( 2 ) gives r 1 r 2 = r 3 ( 4 )
Step 3: To express r 4 in terms of r 3
By Descartes’ Circle Theorem ,
k 4 = k 1 + k 2 + k 3 + k 4 + 2 k 1 k 2 + k 2 k 3 + k 3 k 1 ⇒ r 4 1 = r 1 1 + r 2 1 + r 3 1 + 2 r 1 1 ⋅ r 2 1 + r 2 1 ⋅ r 3 1 + r 3 1 ⋅ r 1 1 ⇒ r 4 1 = r 1 r 2 r 3 r 1 r 2 + r 2 r 3 + r 3 r 1 + 2 r 1 r 2 r 3 r 1 + r 2 + r 3 ⇒ ( 2 ) , ( 4 ) r 4 1 = r 3 2 r 3 + ( 1 − r 3 ) r 3 + 2 r 3 2 1 ⇒ r 4 1 = r 3 4 − r 3 ⇒ r 4 = 4 − r 3 r 3 ( 5 )
Step 4: To find r 1 , r 2 and hence their ratio
Since the sum of all the radii equals 1 1 2 1 1 7 we have r 1 + r 2 + r 3 + r 4 = 1 1 2 1 1 7 ⇒ ( 2 ) 1 + r 4 = 1 1 2 1 1 7 ⇒ ( 5 ) 1 + 4 − r 3 r 3 = 1 1 2 1 1 7 ⇔ r 3 = 1 1 7 2 0 ( 6 ) ( 2 ) ⇒ r 1 + r 2 = 1 − r 3 ⇒ ( 6 ) r 1 + r 2 = 1 1 7 9 7 ( 4 ) 3 ⇒ ( 6 ) r 1 + r 2 = 1 1 7 2 0
Hence, r 1 , r 2 are the roots of the quadratic equation x 2 − 1 1 7 9 7 x + 1 1 7 2 0 = 0 , i.e. r 1 = 9 4 a n d r 2 = 1 3 5 or vice versa.
Finally, the ratio of the larger yellow semicircle’s radius to the smaller yellow semicircle’s radius is 1 3 5 9 4 = 4 5 5 2 For the answer, p = 5 2 , q = 4 5 , thus, p + q = 9 7 .