Dynamic Geometry: P84
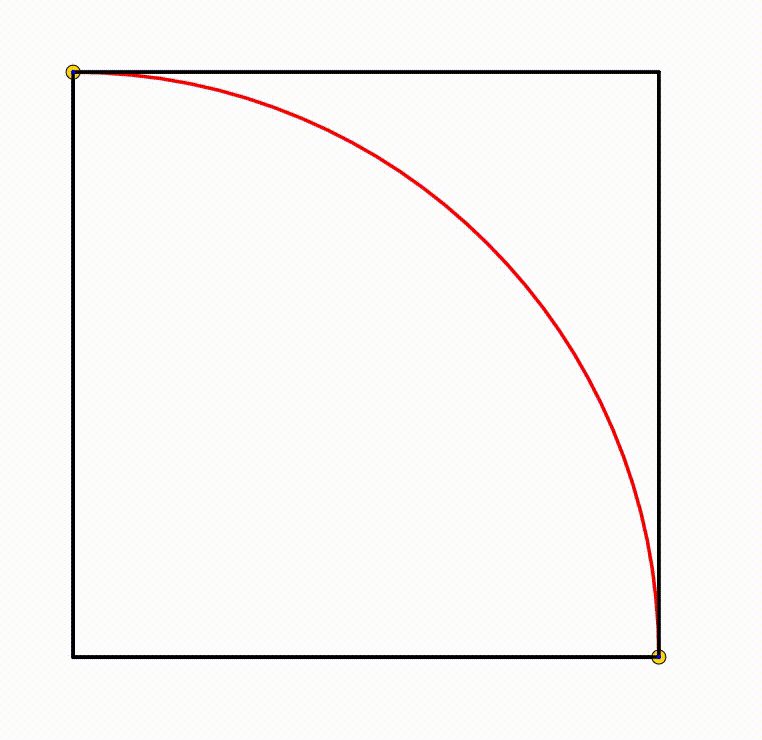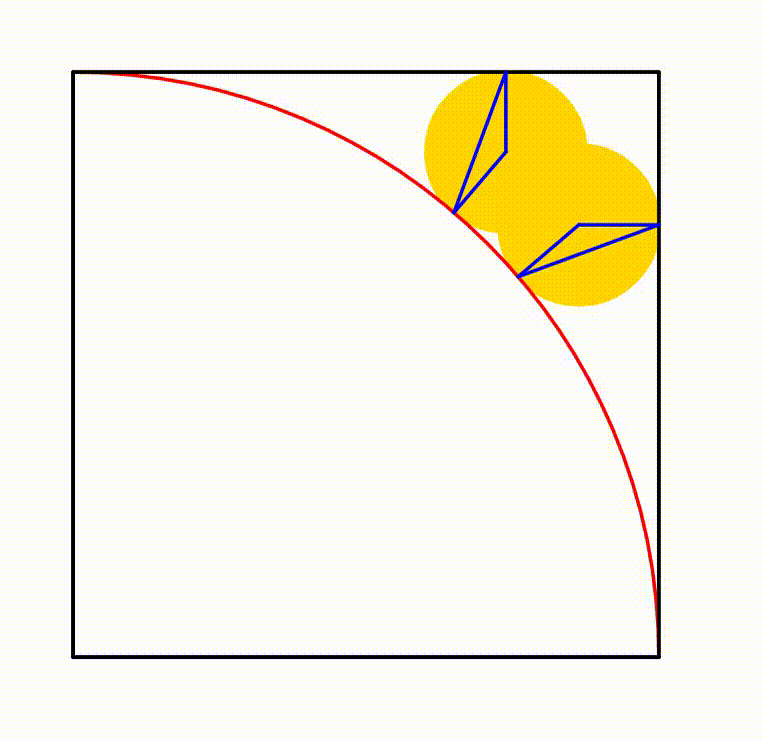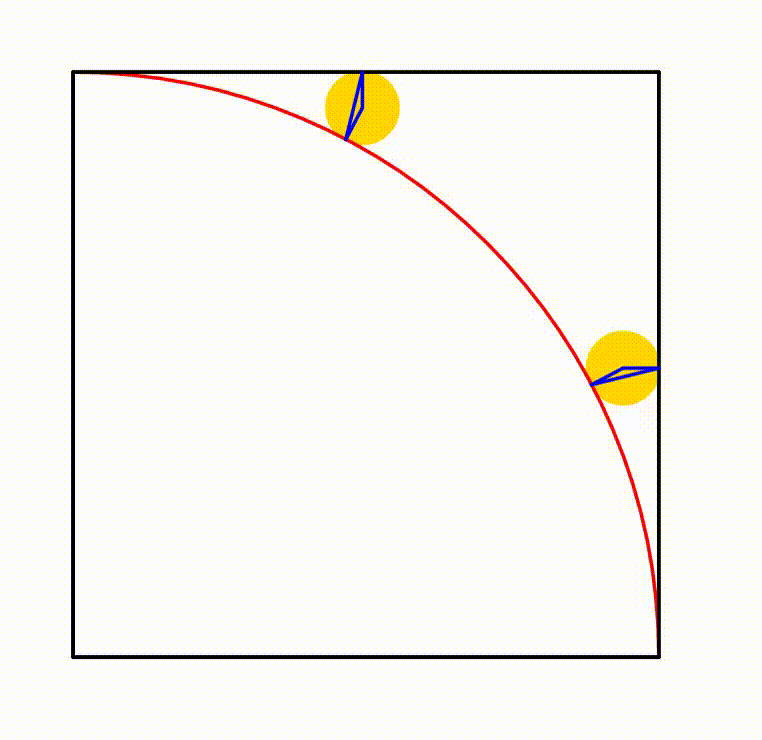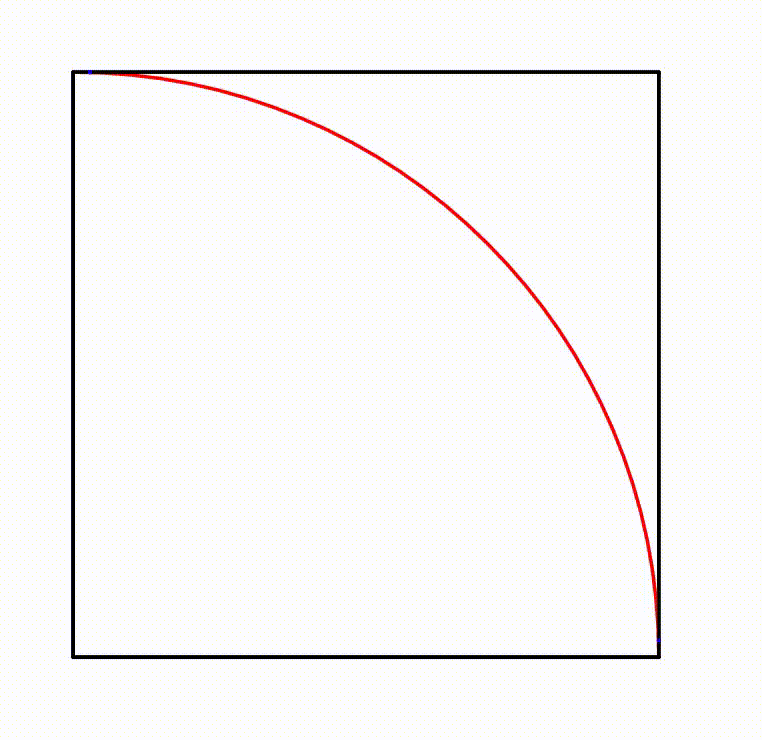 The diagram shows a unit square and a unit quadrant. The yellow circle is any circle which is always tangent to a side of the square and the quadrant. A blue triangle is drawn using the center of a yellow circle and the tangency point between a yellow circle, the square and the quadrant. When the triangle's inradius is equal to
6
0
0
7
, the radius of a yellow circle can be expressed as
q
p
, where
p
and
q
are coprime positive integers. Find
p
+
q
.
The diagram shows a unit square and a unit quadrant. The yellow circle is any circle which is always tangent to a side of the square and the quadrant. A blue triangle is drawn using the center of a yellow circle and the tangency point between a yellow circle, the square and the quadrant. When the triangle's inradius is equal to
6
0
0
7
, the radius of a yellow circle can be expressed as
q
p
, where
p
and
q
are coprime positive integers. Find
p
+
q
.
The answer is 31.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Label the diagram as follows, and let the yellow circle have a radius of R :
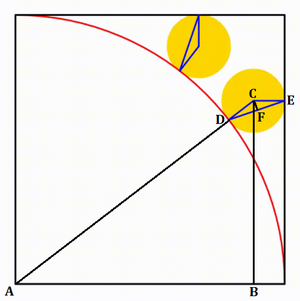
Then A C = 1 + R and A B = 1 − R , and letting θ = ∠ A C B , from △ A B C , sin θ = A C A B = 1 + R 1 − R , so cos θ = 1 − sin 2 θ = 1 + R 2 R .
Let t = ∠ D C F = ∠ E C F . Then from △ C F E , C F = R cos t and F E = R sin t , so that the inradius of △ C D E is r = P △ C D E 2 A △ C D E = C D + C E + D E 2 ⋅ 2 1 ⋅ D E ⋅ C F = R + R + 2 R sin t 2 R sin t ⋅ R cos t = 2 ( sin t + 1 ) R sin 2 t .
But 2 t = ∠ D C E = ∠ A C B + ∠ B C E = θ + 9 0 ° , so sin 2 t = sin ( θ + 9 0 ° ) = cos θ = 1 + R 2 R , and sin t = sin 2 1 ( θ + 9 0 ° ) = 2 1 ( 1 − cos ( θ + 9 0 ° ) ) = 2 1 ( 1 + sin θ ) = 2 1 ( 1 + 1 + R 1 − R ) = 1 + R 1 .
Substituting r = 6 0 0 7 , sin 2 t = 1 + R 2 R , and sin t = 1 + R 1 into r = 2 ( sin t + 1 ) R sin 2 t gives 6 0 0 7 = 2 ( 1 + R 1 + 1 ) R ⋅ 1 + R 2 R = 1 + R + 1 + R R R , which solves to R = 5 7 6 4 9 .
Therefore, p = 4 9 , q = 5 7 6 , and p + q = 7 + 2 4 = 3 1 .
Hi there, thank you for posting !
@Valentin Duringer You really are going to post 100 questions in these series !!! (You really go on your word), Thank you so much for all these questions. A small request can you make the P100 a really difficult one.
Log in to reply
Ok, ok friend, you asked for it, I am cooking something special for you...
Let the square be A B C D , the center of the circle be O , its radius r and two contact points E and F . Let ∠ O A B = θ .
We note that
A O ⋅ cos θ + O F ( 1 + r ) cos θ + r ⟹ r = A B = 1 = 1 + cos θ 1 − cos θ = 1 + 1 + t 2 1 − t 2 1 − 1 + t 2 1 − t 2 = t 2 Let t = tan 2 θ
The inradius of a triangle is given by r i = s A , where A is the area and semi-perimeter of the triangle. Since ∠ O A B = θ , ∠ E O F = 1 8 0 ∘ − θ , and since △ E O F is isosceles, ∠ O E F = O F E = 2 θ and its inradius is:
r i ⟹ r i = s A = r + r cos 2 θ r 2 sin 2 θ cos 2 θ = 1 + cos 2 θ r sin 2 θ cos 2 θ = cos 2 2 θ sin 2 2 θ ⋅ 1 + cos 2 θ sin 2 θ cos 2 θ = cos 2 θ 1 − cos 2 2 θ ⋅ 1 + cos 2 θ sin 2 θ = cos 2 θ sin 2 θ ( 1 − cos 2 θ ) = tan 2 θ ( 1 − cos 2 θ ) = t ( 1 − 1 + t 2 1 ) Note that r = t 2 = tan 2 2 θ Since 1 + tan 2 ϕ = sec 2 ϕ
When r i = 6 0 0 7 :
t ( 1 − 1 + t 2 1 ) 6 0 0 t − 7 ( 1 + t 2 ) ( 6 0 0 t − 7 ) 2 3 6 0 0 0 0 t 4 − 8 4 0 0 t 3 + 4 9 t 2 − 8 4 0 0 t + 4 9 ( 2 4 t − 7 ) ( 1 5 0 0 0 t 3 + 4 0 2 5 t 2 + 1 1 7 6 t − 7 ) ⟹ t ⟹ r = 6 0 0 7 = 1 + t 2 6 0 0 t = 6 0 0 2 t 2 = 0 = 0 = 2 4 7 = t 2 = 2 4 2 7 2 The other irrational root ≈ 0 . 0 0 5 8 3 3 4 is too small.
Therefore p + q = 7 + 2 4 = 3 1 .