Dynamic Geometry: P87
 The diagram shows a semicircle with radius
1
. The cyan square moves freely so it is always internally tangent to the semicircle. The center of the square traces a
locus
(purple curves). The area bounded by the semicircle's diameter and the curves can be expressed as:
The diagram shows a semicircle with radius
1
. The cyan square moves freely so it is always internally tangent to the semicircle. The center of the square traces a
locus
(purple curves). The area bounded by the semicircle's diameter and the curves can be expressed as:
q p tan − 1 ( q )
where p and q are positive integers. q is a prime. Find p + q .
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
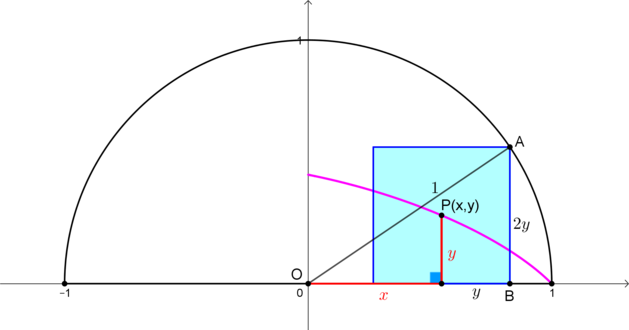 Consider the purple curve in the first quadrant. Let
(
x
,
y
)
be the coordinates of the center
P
of the square. Then, referring to the figure,
O
D
=
x
+
y
and
C
D
=
2
y
.
Consider the purple curve in the first quadrant. Let
(
x
,
y
)
be the coordinates of the center
P
of the square. Then, referring to the figure,
O
D
=
x
+
y
and
C
D
=
2
y
.
By Pythagorean theorem on △ O C D , O A 2 = O B 2 + A B 2 ⇒ 1 = ( x + y ) 2 + ( 2 y ) 2 which solves, for y ≥ 0 , to y = 5 1 ( 5 − 4 x 2 − x ) The area A 1 bounded by the semicircle's diameter and the purple curve in the first quadrant is A 1 = 5 1 0 ∫ 1 ( 5 − 4 x 2 − x ) = 5 1 0 ∫ 1 5 − 4 x 2 d x − 5 1 0 ∫ 1 x d x = 5 2 0 ∫ 1 4 5 − x 2 d x − 1 0 1 = 5 2 ⎝ ⎜ ⎛ ⎣ ⎡ 2 1 x 4 5 − x 2 + 2 1 ⋅ 4 5 tan − 1 4 5 − x 2 x ⎦ ⎤ 0 1 ⎠ ⎟ ⎞ − 1 0 1 = 4 1 tan − 1 2 Due to symmetry, the total area bounded by the semicircle's diameter and the curves is A = 2 A 1 = 2 1 tan − 1 2 For the answer, p = 1 , q = 2 , thus, p + q = 3 .
Let the center of the unit semicircle be O ( 0 , 0 ) , the origin of the x y -plane, and an arbitrary point on the locus or the center of the square be P ( x , y ) when the square has a side length of a . We note that
⎩ ⎨ ⎧ y = 2 a x = 1 − a 2 − 2 a = 1 − 4 y 2 − y
The area under the locus is given by:
A = 2 ∫ 0 5 1 x d y = 2 ∫ 0 5 1 ( 1 − 4 y 2 − y ) d y = 2 ∫ 0 5 1 1 − 4 y 2 d y − 2 ∫ 0 5 1 y d y = ∫ 0 sin − 1 5 2 cos 2 θ d θ − y 2 ∣ ∣ ∣ ∣ 0 5 1 = ∫ 0 tan − 1 2 2 1 + cos 2 θ d θ − 5 1 = 2 θ + 4 sin 2 θ ∣ ∣ ∣ ∣ 0 tan − 1 2 − 5 1 = 2 tan − 1 2 + 5 1 − 5 1 = 2 tan − 1 2 Note that when x = 0 , y = 5 1 Let y = 2 sin θ ⟹ d y = 2 cos θ d θ
Therefore p + q = 1 + 2 = 3 .