Dynamic Geometry: P91
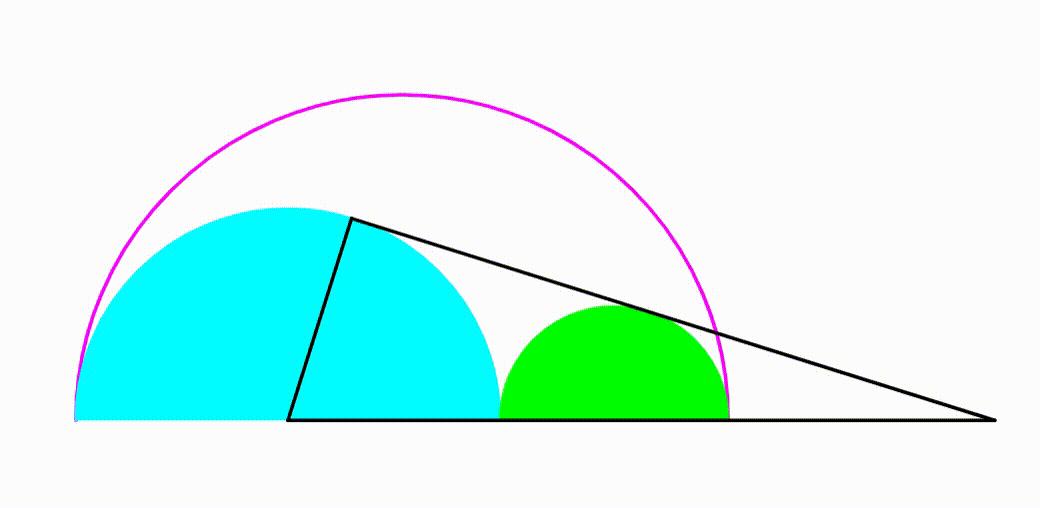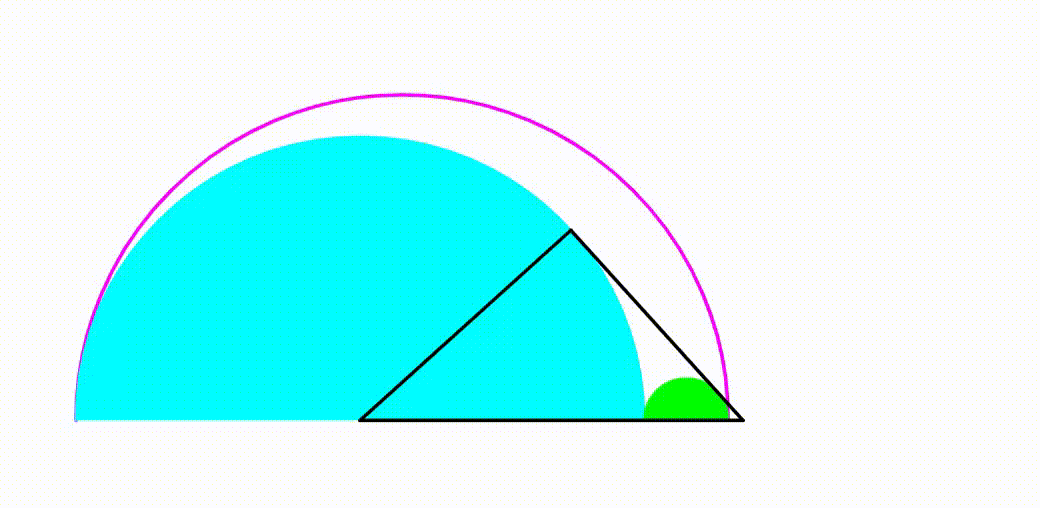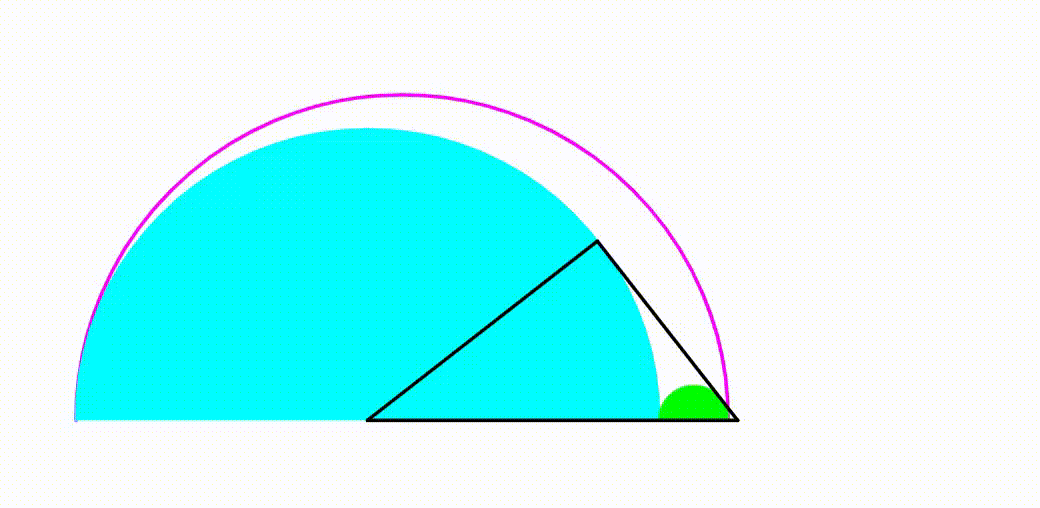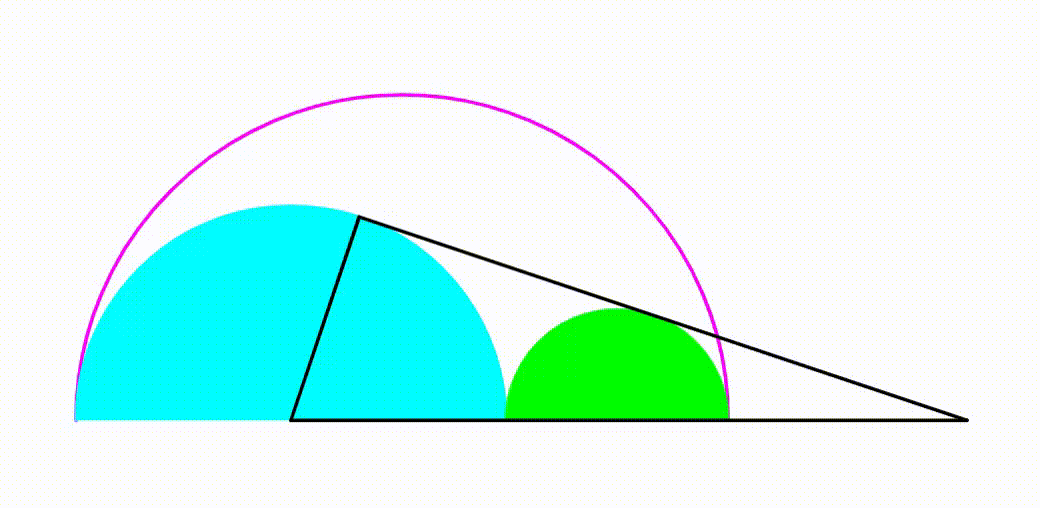 The diagram shows a purple semicircle with radius
. The cyan and the green semicircle are tangent to each other and internally tangent to the purple semicircle. They are growing and shrinking freely so that the sum of their radius is always equal to the purple semicircle's radius. The right black triangle has one leg tangent to both semicircles and one leg is the radius of the cyan circle. When the ratio of its perimeter to its area is equal to
, the ratio of the cyan circle's radius to the radius of the green radius can be expressed as
, where
and
are coprime positive integers. Find
.
The diagram shows a purple semicircle with radius
. The cyan and the green semicircle are tangent to each other and internally tangent to the purple semicircle. They are growing and shrinking freely so that the sum of their radius is always equal to the purple semicircle's radius. The right black triangle has one leg tangent to both semicircles and one leg is the radius of the cyan circle. When the ratio of its perimeter to its area is equal to
, the ratio of the cyan circle's radius to the radius of the green radius can be expressed as
, where
and
are coprime positive integers. Find
.
Note : the radius of both green and cyan semicircles have to be rationnal.
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the radius of the large semicircle be 1 and its diameter F G , the centers and radii of the cyan and green be A and D , and r and r 1 respectively, the triangle in question be A B C , D E be tangent to B C , and G B = k .
We note that r + r 1 = 1 and that △ A B C and △ B D E are similar. Then
D B A B r 1 + k r + 2 r 1 + k 1 − r + k 2 − r + k 2 k r − k ⟹ k = D E A C = r 1 r = 1 − r r = 2 r 2 − 4 r + 2 = 2 r − 1 2 ( 1 − r ) 2 Since r + r 1 = 1
Then A B = A G + G B = 2 − r + k = 2 r − 1 r . By Pythagorean theorem , B C = A B 2 − A C 2 = ( 2 r − 1 ) 2 r 2 − r 2 = 2 r − 1 2 r r − r 2 . Then the ratio of perimeter to area of △ A B C is:
A C ⋅ B C / 2 A C + A B + B C r ⋅ 2 r − 1 r r − r 2 r + 2 r − 1 r + 2 r − 1 2 r r − r 2 2 r r − r 2 2 r − 1 + 1 + 2 r − r 2 r r − r 2 r + r − r 2 = 3 6 0 2 8 7 3 = 3 6 0 2 8 7 3 = 3 6 0 2 8 7 3 = 7 2 0 2 8 7 3
Solving for r , we get r = 1 6 9 1 4 4 and r = 5 7 4 6 1 8 6 5 ± 5 7 4 6 5 4 1 7 8 5 . Taking the rational value, then the ratio of radii of the two smaller semicircles
r 1 r = 1 − 1 6 9 1 4 4 1 6 9 1 4 4 = 2 5 1 4 4
Therefore 1 4 4 + 2 5 = 1 6 9 = 1 3 .