Dynamic Geometry: P97
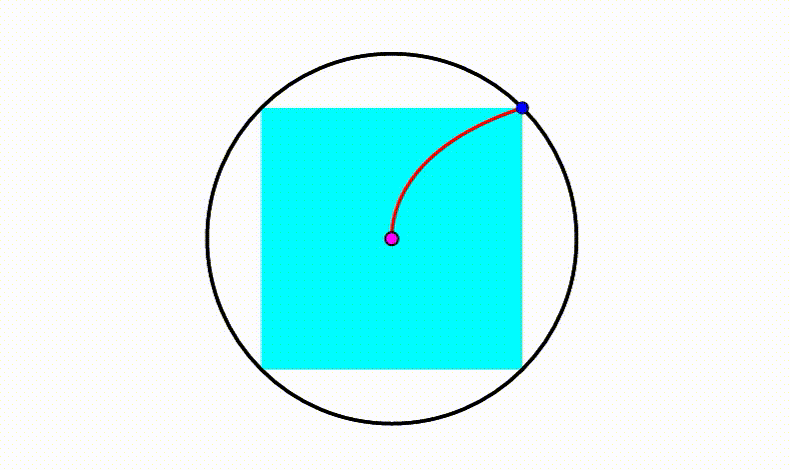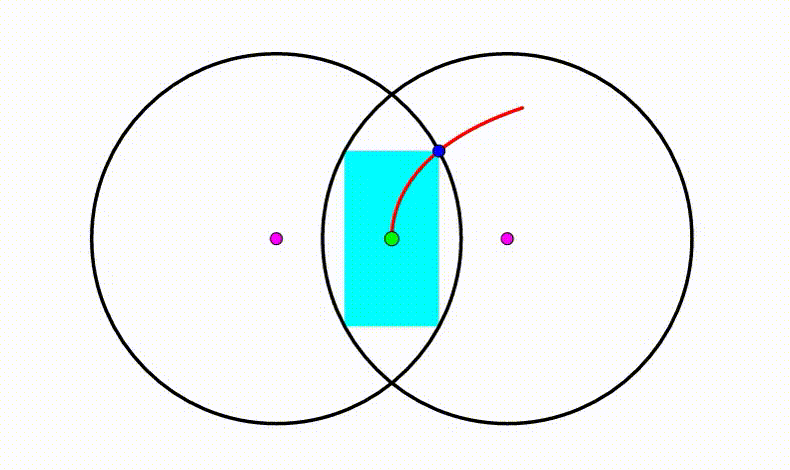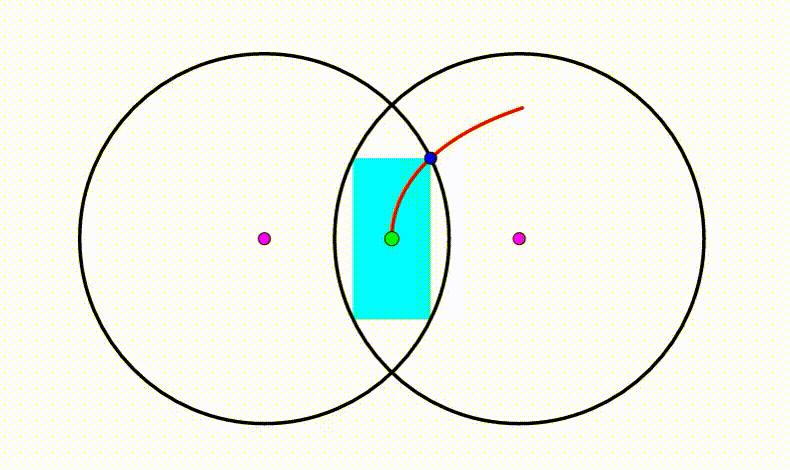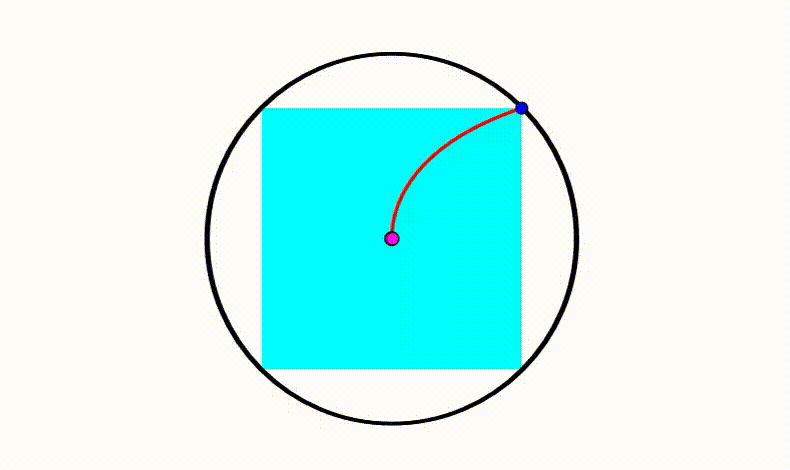 The diagram shows two black circles with radius
. Their centers (purple points) move appart horizontaly. The cyan rectangle is inscribed in the overlapping space between the two circles. It is always the rectangle which area is
maximum
. The blue point traces a
locus
(red curve). If the green point is the origin is a coordinate system, the equation of the locus can be written as:
The diagram shows two black circles with radius
. Their centers (purple points) move appart horizontaly. The cyan rectangle is inscribed in the overlapping space between the two circles. It is always the rectangle which area is
maximum
. The blue point traces a
locus
(red curve). If the green point is the origin is a coordinate system, the equation of the locus can be written as:
where and are positive integers. Find .
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let an arbitrary point on the locus be P ( x , y ) and the distance of the center either circle to the origin ( 0 , 0 ) of the x y -plane be a . By Pythagorean theorem ,
( x + a ) 2 + y 2 = 1 2 ⟹ y = 1 − ( x + a ) 2
And the area of the rectangle is A = 4 x y = 4 x 1 − ( x + a ) 2 . To find the relation between x and y , when A is maximum,
d x d A 1 − ( x + a ) 2 1 − ( x + a ) 2 ( x + a ) 2 + x ( x + a ) − 1 a 2 + 3 a x + 2 x 2 − 1 ⟹ a = 4 1 − ( x + a ) 2 − 1 − ( x + a ) 2 4 x ( x + a ) = 1 − ( x + a ) 2 x ( x + a ) = x ( x + a ) = 0 = 0 = 2 x 2 + 4 − 3 x Putting d x d A = 0 or y 2 = x ( x + a ) Solving the quadratic for a Since a > 0
Since y 2 = x ( x + a ) = x 2 + x ⋅ 2 x 2 + 4 − 3 x = 2 x 2 + 4 − x 2 ,
⟹ y = 2 x 2 + 4 − x 2
Therefore p + q = 4 + 2 = 6 .