Dynamic Square Geometry
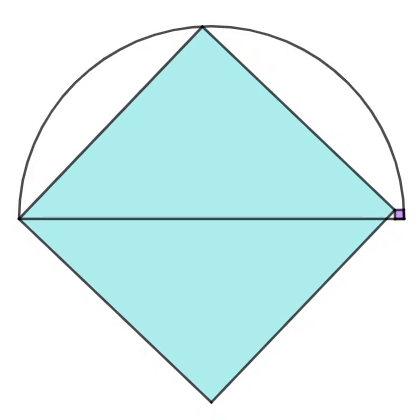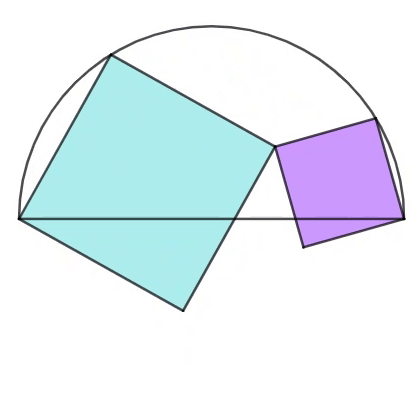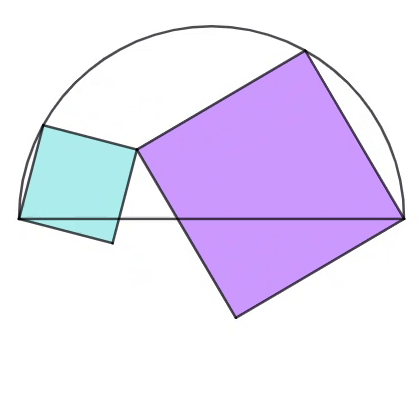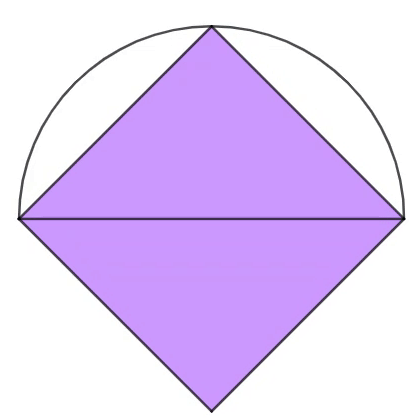
The diagram shows two tangential squares whose vertex exists at the endpoint of the diameter of semicircle of unit radius length. As their vertices on the circumference move counterclockwise, the cyan square decreases in size, whereas the purple square increases in size.
Find the area sum of the cyan and the purple squares at the moment when the center of the semicircle lies on the perimeter of the purple square.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the side length of the purple and cyan square be x and y , respectively.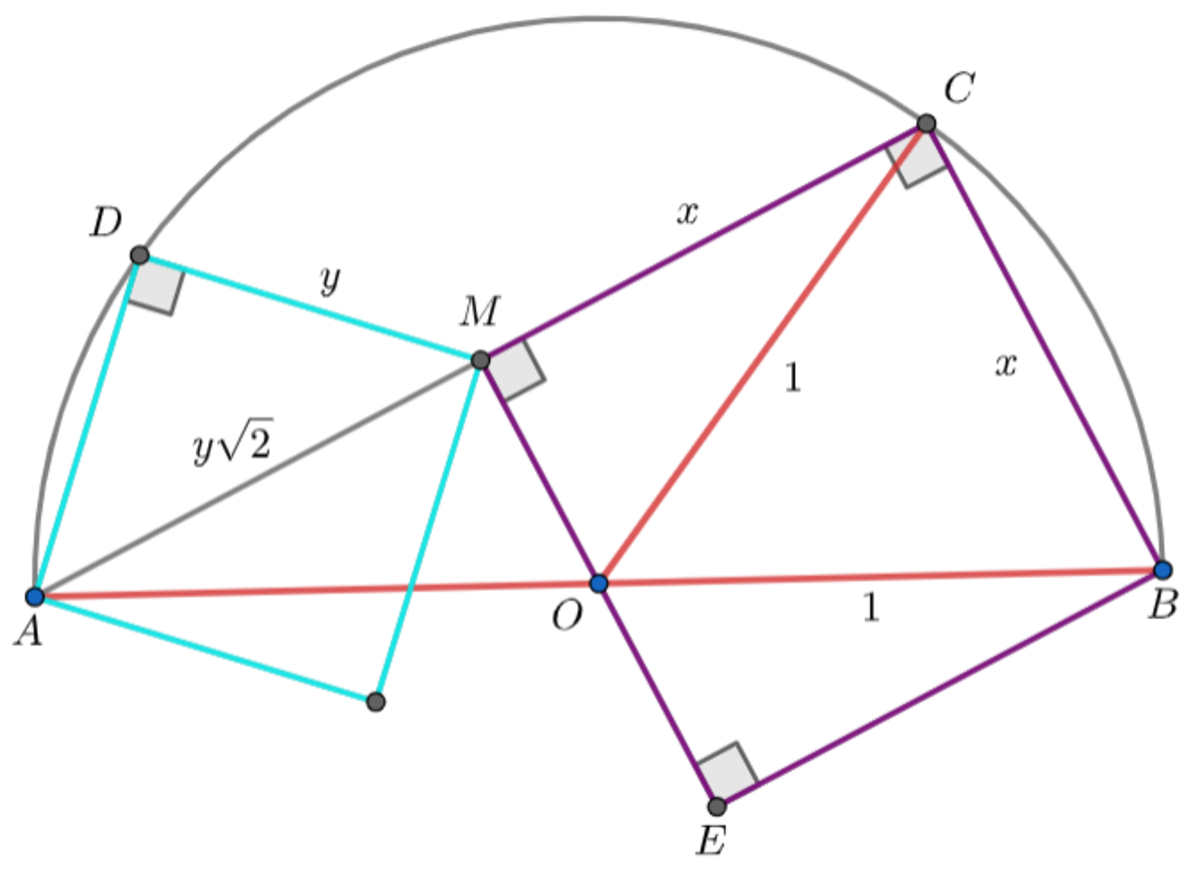 Since,
C
M
=
B
E
=
x
,
∠
B
E
O
=
∠
C
M
O
=
9
0
∘
and
O
C
=
O
B
=
1
, by
RHS congruence criterion
,
△
C
M
O
≅
△
B
E
O
⟹
O
E
=
O
M
=
2
x
Using the
Pythagorean Theorem
, in
△
C
M
O
,
O
M
2
+
C
M
2
4
x
2
+
x
2
∴
x
=
O
C
2
=
1
=
5
2
Note,
∠
A
C
B
=
∠
M
C
B
=
9
0
∘
since angle in a semicircle is right angle and
M
C
B
E
is a square. Hence, the points
A
,
M
,
C
are collinear and
M
is the foot of the perpendicular from the center
O
to the chord
A
C
. Therefore,
M
A
y
2
∴
y
=
M
C
=
x
=
5
2
The sum of the area of the two squares is,
x
2
+
y
2
=
5
4
+
5
2
=
5
6
Since,
C
M
=
B
E
=
x
,
∠
B
E
O
=
∠
C
M
O
=
9
0
∘
and
O
C
=
O
B
=
1
, by
RHS congruence criterion
,
△
C
M
O
≅
△
B
E
O
⟹
O
E
=
O
M
=
2
x
Using the
Pythagorean Theorem
, in
△
C
M
O
,
O
M
2
+
C
M
2
4
x
2
+
x
2
∴
x
=
O
C
2
=
1
=
5
2
Note,
∠
A
C
B
=
∠
M
C
B
=
9
0
∘
since angle in a semicircle is right angle and
M
C
B
E
is a square. Hence, the points
A
,
M
,
C
are collinear and
M
is the foot of the perpendicular from the center
O
to the chord
A
C
. Therefore,
M
A
y
2
∴
y
=
M
C
=
x
=
5
2
The sum of the area of the two squares is,
x
2
+
y
2
=
5
4
+
5
2
=
5
6