Dynamic Triangle Geometry

Geometry Level 3

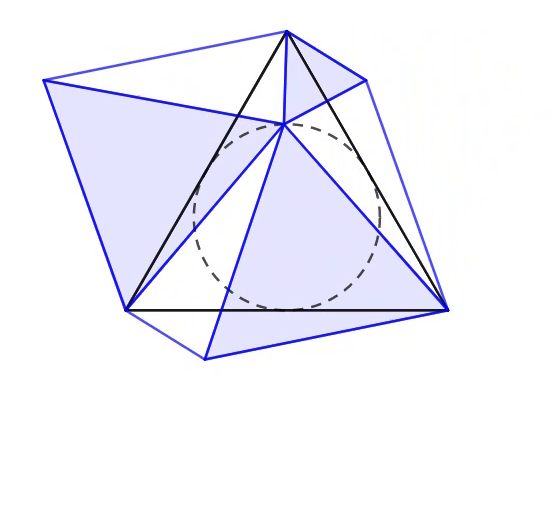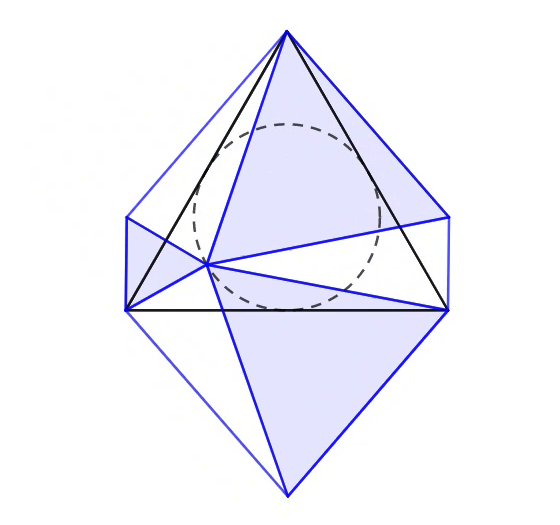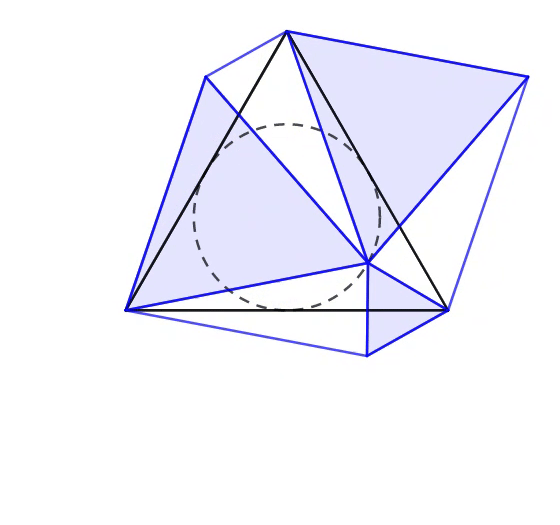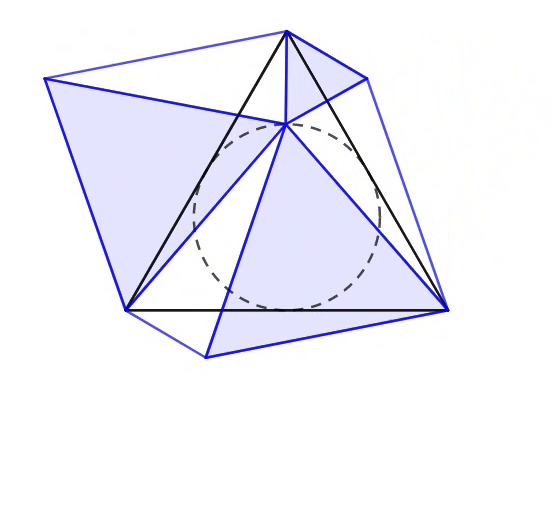
In the animation above, each of the smaller equilateral triangles is extended from the respective vertex of the large equilateral triangle, such that the three triangles touch each other exactly at the circumference of the incircle. The three segments each connect two vertices of equilateral triangles.

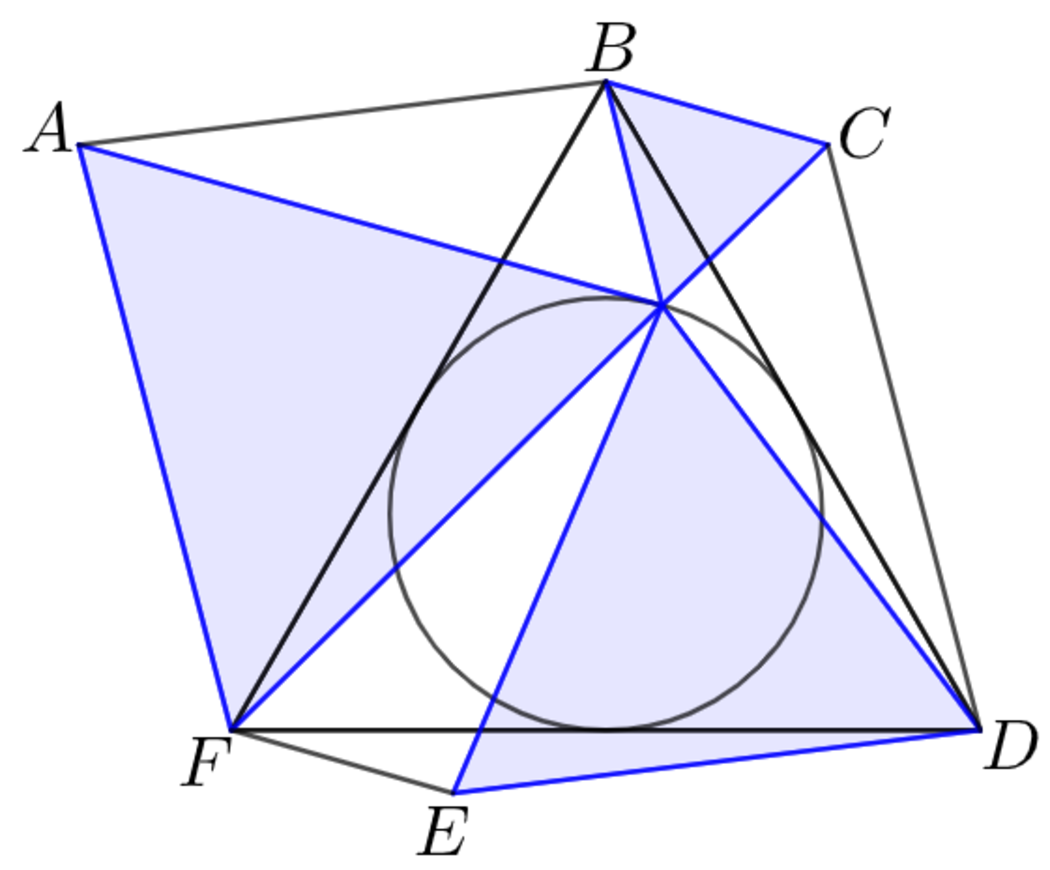
What is the area ratio of the sum of three shaded regions to the area of $ABCDEF$ ?

\dfrac{1}{2}

\dfrac{5}{8}

\dfrac{2}{3}

\dfrac{3}{4}

\dfrac{5}{6}

\dfrac{7}{8}

The ratio depends on the position of the intersection point. There exists the unique ratio, but not in the choices given.

1 solution

Xiao Simon
Mar 27, 2021

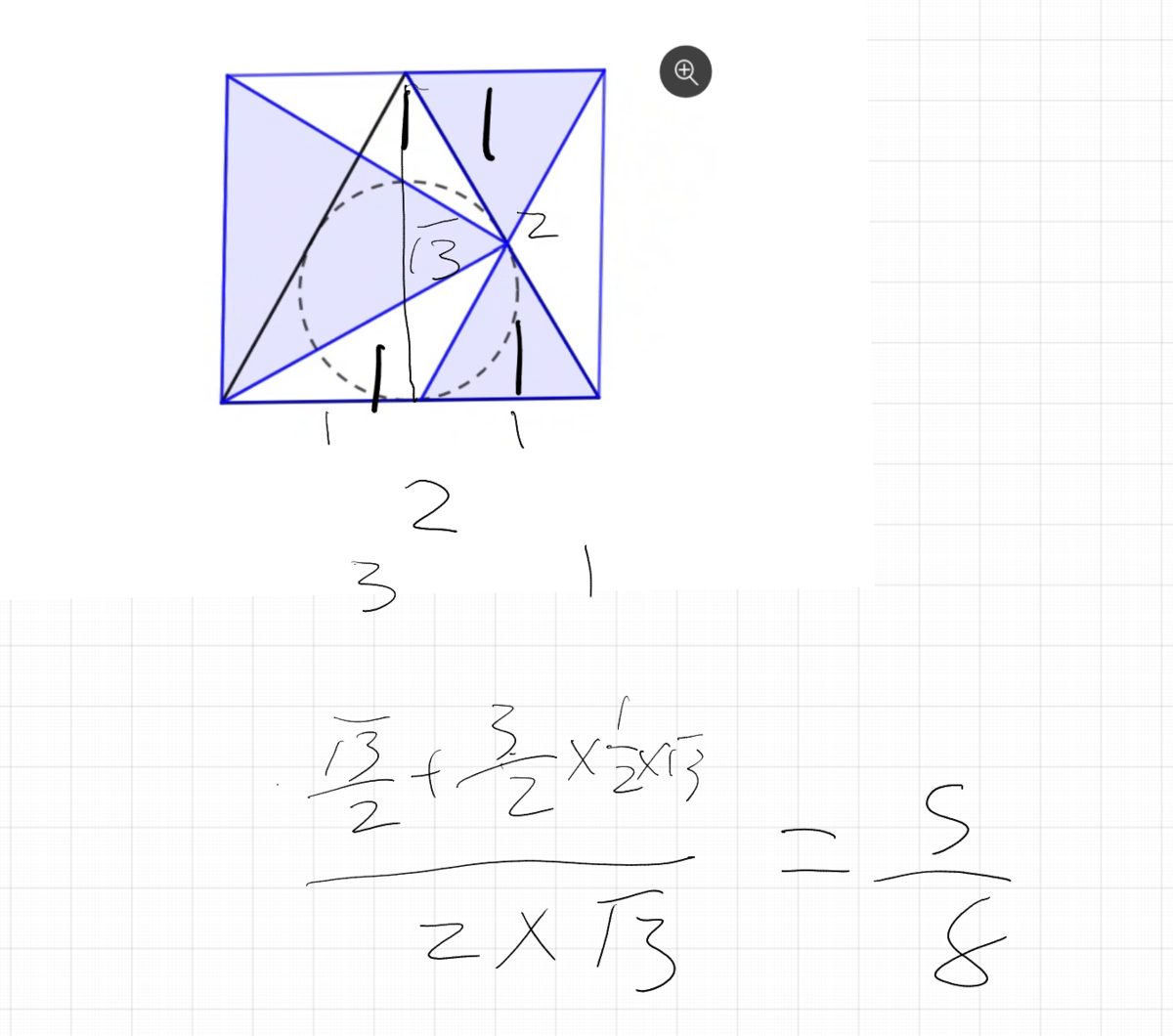this is probably not a very rigorous solution but i realized how symmetrical i can make the problem so i paused at that moment and solved it

but please can someone explain here how the ratio doesn't depend on the intersection points. THanks

Xiao Simon - 2 months, 2 weeks ago

Hint: Condition $r$ to be the inradius and then, apply Law of Cosines . Do you know where this is heading?

Michael Huang - 2 months, 2 weeks ago

Dynamic Triangle Geometry

1 solution

0 pending reports