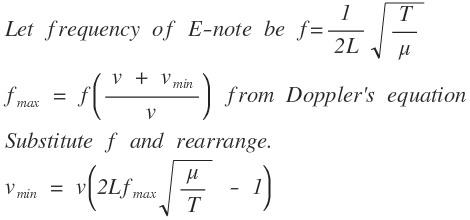E-note and Doppler effect

Classical Mechanics Level 3

The high “E-note” string on a guitar has a linear mass density of μ . \mu . It is tightened between two fixed points a distance L L apart to a tension of T . T. A performer on a stage plays this E-note at the same time as a fast spectator rushes toward the stage at high speed. What is the minimum speed the spectator must go so that the frequency he observes is above the human range of hearing, f m a x ? f_{max} ? Please express your answer in terms of numerical constants and any of the following: μ , L , T , f m a x \mu , L, T, f_{max} and the speed of sound in air, v . v.

v m i n = v L ( 2 f m a x μ T − 1 ) v_{min} = \frac{v}{L} \left( 2f_{max}\sqrt{\frac{\mu}{T}}-1 \right) v m i n = 2 v ( 2 L f m a x μ T − 1 ) v_{min} = 2v \left( 2Lf_{max}\frac{\mu}{T}-1 \right) v m i n = v ( 2 L f m a x μ T − 1 ) v_{min} = v \left( 2Lf_{max}\sqrt{\frac{\mu}{T}}-1 \right) v m i n = v ( 2 L f m a x μ T − 1 ) v_{min} = v \left( 2Lf_{max}\sqrt{\mu T}-1 \right)

Srinivasa Satti by Srinivasa Satti

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Aman Deep Singh
Dec 25, 2015

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...