Easier 5x5 lattice resistor problem. What is product of most common voltage & number of such nodes?

Electricity and Magnetism Level 3

All resistors are 1 Ω 1\Omega . Input node is #3 at 1V. Output node is #23 at 0V (grounded).

This variant of the 5x5 resistor lattice problem is very much easier. It can be answered without doing any computation if you consider well the symmetries of the lattice.

Determine the most common node voltage relative to ground and the number of nodes at that voltage.

The answer is the product of that voltage and the number of such nodes. What is the answer ?


The answer is 2.5.

A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Steven Chase
Feb 18, 2019

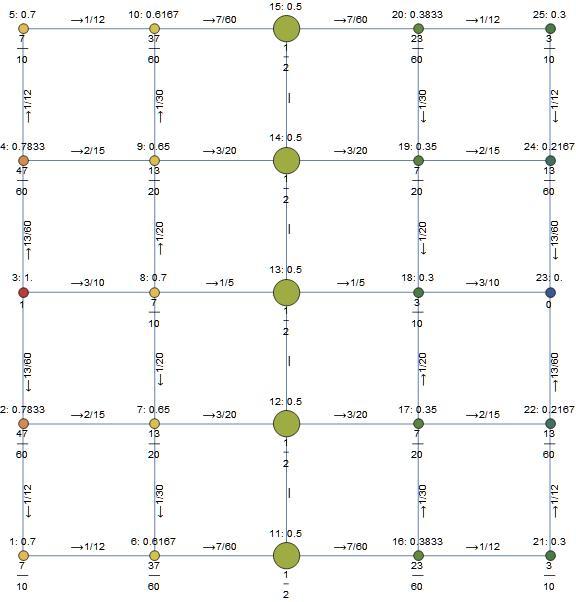
Node voltages are shown below. There are five nodes at half a volt, so the answer is 2.5

2 Helpful 0 Interesting 0 Brilliant 0 Confused

Thank you for triggering a bit of research into how to write a fairly general Kirchhoff's voltage and current Laws solution in Mathematica. I gave you an up vote for that reason.

A Former Brilliant Member - 2 years, 3 months ago

Thanks. That sounds like a useful endeavor. You may be amused to learn that my solution was not a general one. I wrote out the equations (matrix entries) for this specific network.

Steven Chase - 2 years, 3 months ago

I do not know what happened to my original explanation. When I compared mine to Steven Chase's solution to that disappeared explanation, I noticed that some of the voltages were different than the results I had computed using a mesh analysis and approximating the voltages assuming a voltage divider relationship. I spent most of the last three days writing a Kirchhoff's laws solution In Mathematica to determine the correct answer . With the currents that Kirchhoff's laws solution provided, I computed the voltage drops across the resistors. Steven Chase's answer is correct. My first approximation answers were wrong . The answers above are from the Kirchhoff's Laws solution. My approximation did not change the problem's answer that was asked.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...