Easier than snot

As line $y = x$ intersects line $x + 2y = 3$ at $P(1, 1)$ , line $y = ax - b$ must go through $P$ too, so $\\ 1 = a \times 1 - b \implies a - b = 1$

When line $l_1,\; y=x$ is reflected over line $l_2,\; x+2y=3,$ every point that lies on $l_1$ is reflected over $l_2$ . So the point of intersection of $l_1$ and $l_2$ will also lie on the reflected line, $y=ax-b$ .

Solving the pair of equations, $\begin{cases} y=x \\ x+2y=3\end{cases}$ gives us the intersection point, $(1,1)$ . As stated earlier, the point $(1,1)$ satisfies the equation of the line $y=ax-b$ .

Therefore, $1=1\cdot a-b\implies a-b=\boxed{1}$

---

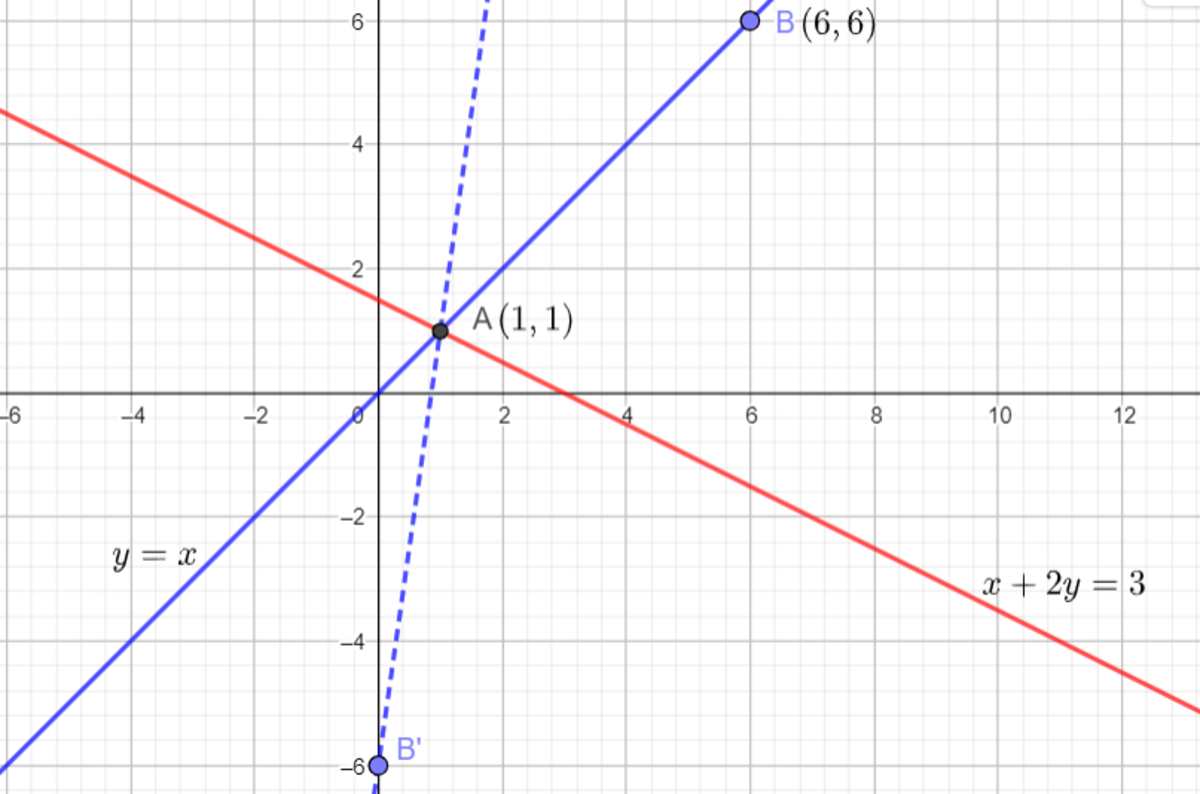
Note: A more general approach would be to find two points on the reflected line, since two points define a unique line. We pick a point, say $B(6,6)$ , and reflect it over $l_2$ . As shown here , the reflected point is $B'(0,-6)$ . Since we know that the two points $A(1,1)$ and $B'(0,-6)$ lie on the reflected line, using the point-point form of a line, the required equation is, $y-1=\frac{1-(-6)}{1-0}{(x-1)}$ $\implies y=7x-6$