easiest

Algebra Level 1

There are 25 students in the class. Each student attends a sport class or an art school. Some of students attend both a sport class and an art school. Number of the students attending a sport class is 18; number of the students attending an art school is 12. How many of class students attend both a sport class and an art school?


The answer is 5.

Adityaraj Modhsaraf by Adityaraj Modhsaraf , 23, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Luciano Canela
Jan 6, 2015

You can use this idea: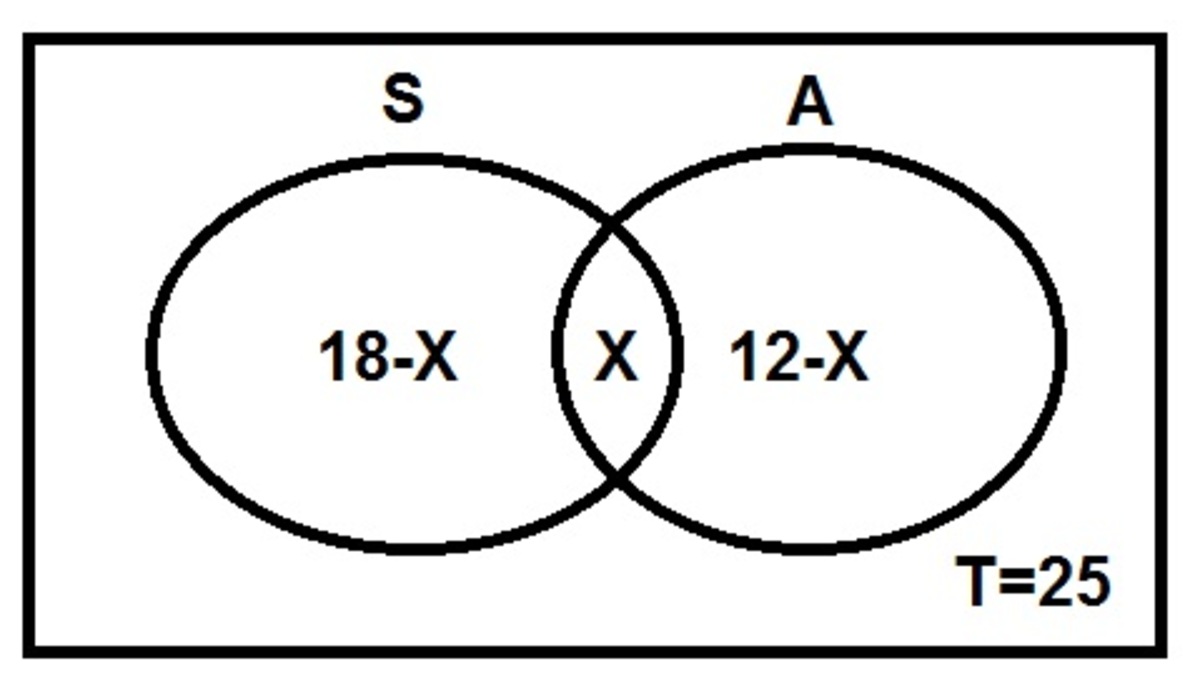

Where:

18-X is the number of students who only attends sport class, 12-X is the number of students that only attends the art school, X is the number of students who attend both, and T is the total of students.

Thus,

18-X + 12-X + X = 25

30 - X = 25

X = 5

2 Helpful 0 Interesting 0 Brilliant 0 Confused

Add the number of all students attending a sport class and the number of all students attending an art school. You will get the total number of students in the class plus the number of those students who attend both a sport class and an art school because you included twice to this sum those students who attend both a sport class and an art school.

It follows from this counting that the number of students who attend both a sport class and an art school, is equal to (18 + 12) - 25 = 30 - 25 = 5.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

If 18 people attend a sports class

and 12 people attend art school

so 30 students totally

but the number of students in the class is 25

some people must be attending 2 classes

there are 5 extra students not extra but simply 5 students attending 2 classes

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...