A geometry problem by Rohit Sharma

I did it this way $3x-4y+12=0\quad \quad \\ \\ 3x=4y-12\\ \\ x=\frac { 4 }{ 3 } y\boxed { -4 } \\ \\ x\quad intercept\quad (-4,0)\\ \\ \\ Then\quad for\quad y\quad intercept\quad \\ \\ 3x-4y+12=0\\ \\ -4y=-3x-12\\ \\ y=\frac { 3 }{ 4 } x\boxed { +3 } \\ \\ y\quad intercept\quad (0,3)\\ \\ \sqrt { { ({ x }_{ 2 }^{ }-{ x }_{ 1 }^{ }) }^{ 2 }+{ ({ y }_{ 2 }^{ }-{ y }_{ 1 }^{ }) }^{ 2 } } \\ \\ \sqrt { { (0-(-4)) }^{ 2 }+{ (3-0) }^{ 2 } } \\ =\sqrt { { 4 }^{ 2 }+{ 3 }^{ 2 } } =\sqrt { 25 } =\quad 5$

Refer to the following graph:

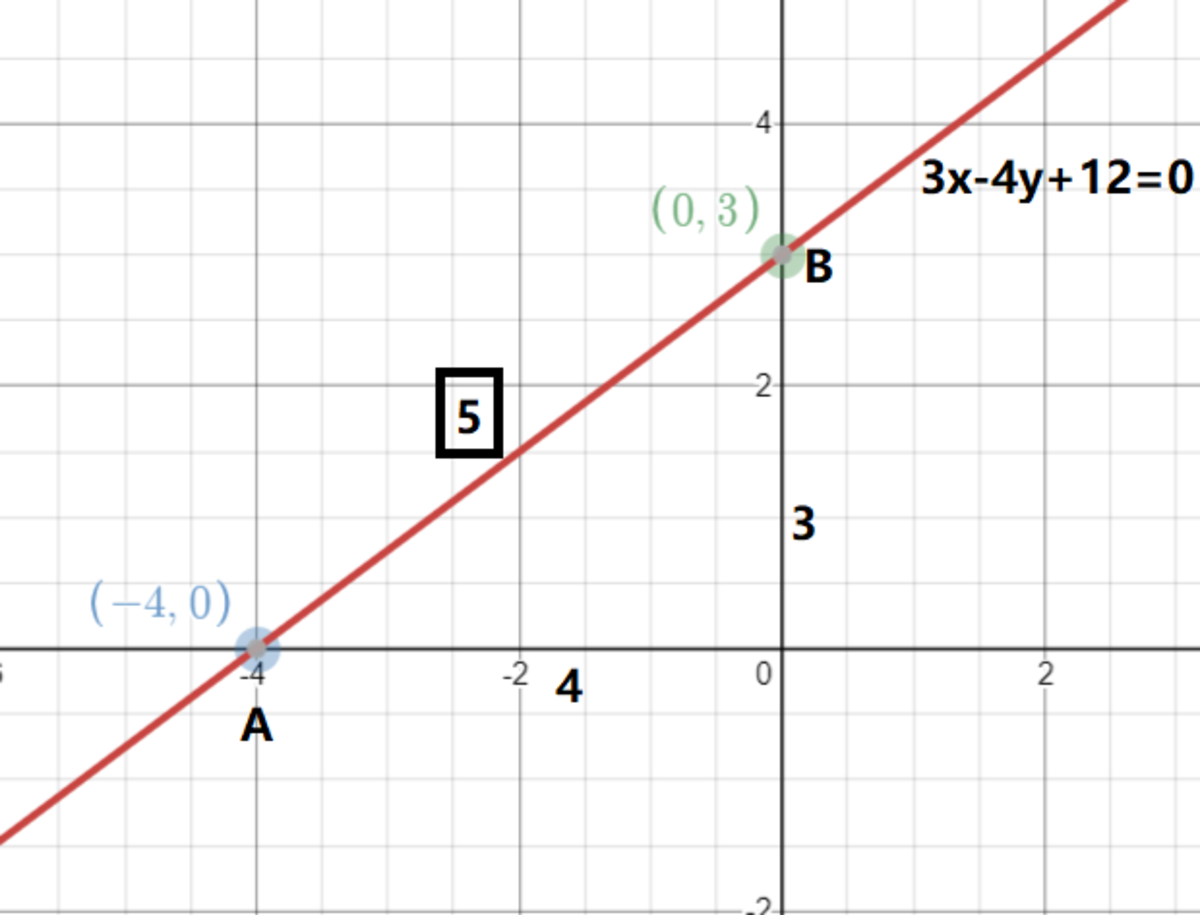Clearly, $AB=5$

$\dfrac{x}{3}-\dfrac{y}{4}=1~~implies~A(3,0)~and B(0,4)\\\therefore~AB=\sqrt{3^2+4^2} = 5.\\$
You may refer to the notes on st. lines in Brilliant.