There's A Really Simple Solution

Algebra Level 1

$\large \text{If } \hspace{.1cm} {x + y = xy = 3}, \hspace{.05cm} {\text{ then evaluate }} \hspace{.1cm} {x^3 + y^3}.$

(Note: the intersections of the system involve complex numbers but they are unnecessary to work out ${x^3 + y^3}.$ )

0 3 4 8

6 solutions

Dev Sharma
Sep 22, 2015

$(x + y)^{3} = 27$

$x^3 + y^3 + 3xy(x + y) = 27$

$x^3 + y^3 = 0$

Nice solution. Another solution could be
x^3 + y^3

= (x+y) (x^2 + y^2 - xy)

= 3 * [(x+y)^2 - 3xy]

= 3 * (9-9)

Eddy Li - 5 years, 8 months ago

i use c.. hahaha

Joel Hukubun - 5 years, 8 months ago

Should be $3(x+y)[(x+y)^2-3xy]$ in the third line.

Jake Lai - 5 years, 8 months ago

No it is meant to be (x+y) immediately subbed into 3 and then you do the rest.

Eddy Li - 5 years, 8 months ago

What is x and y?

wolf 454 - 5 years, 8 months ago

You don't necessarily have to know what x and y are in order to solve the problem, but they would indeed be complex numbers.

Sam Maltia - 5 years, 8 months ago

the values are complex x=3+root3 i/2 and y=3root3 i-3/2

Harshi Singh - 5 years, 8 months ago

Not sure how y'all read this, I read it as X+Y is equal to X*Y which equals 3 So you would be solving for x and y

Matthew Napier - 5 years, 8 months ago

Are you saying this to me???

Harshi Singh - 5 years, 8 months ago

Sushil Kumar
Sep 24, 2015

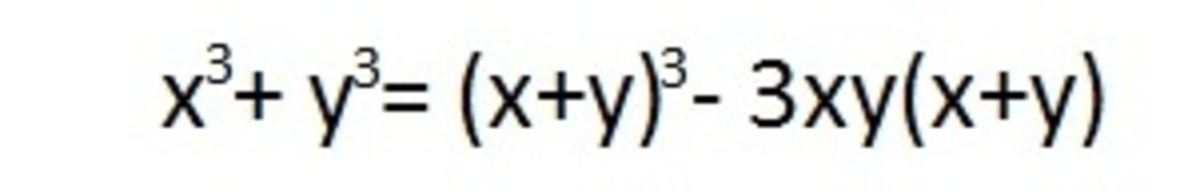substitute the values and get the answer

Raj N
Sep 28, 2015

x^3+y^3 = (x+y)^3 - 3xy(x+y) given : x+y =3 and xy = 3 so putting these values in equation we get, x^3+y^3 = (3)^3 - 3×3(3) = 27 - 27 = 0. Simple....!!!

Oksana Mytsavka
Nov 30, 2016

(x+y)^2=9 x^2+2xy+y^2=9 x^2+y^2=3 x^3+y^3=(x+y)(x^2-xy+y^2)=(3)(3-3)=0

Omar El Amrani
Dec 5, 2015

Can someone tell me how even x and y exist(don't worry i solved it, was pretty easy tho), (note that i still don't know what complex numbers are, so if its possible in C then srry

I saw those problem as invalid, since at least in the realm of real numbers, x+y=xy = 3 is impossible.

James Campbell - 4 years, 11 months ago

Akarsh Anilkumar
Sep 24, 2015

(x+y)^3=x^3+x^2y+xy^2+y^3 (x^3+y^3)=(x+y)^3-x^2y-xy^2 =3^3-3×3×3=0

There's A Really Simple Solution

6 solutions

0 pending reports