Easy Angles 2
In △ A B C , ∠ A is 3 0 ∘ and ∠ B is 8 0 ∘ . What is the measure of the complement of ∠ C in degrees?
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
"The compliment" is not frequently used.
Indeed but you learn something new every day
How is this a "Level 3" problem? Isn't some levelheadedness required here?
\[\begin{align} \angle A + \angle B + \angle C &= 180^{\circ} \\ (30^{\circ}) + (80^{\circ}) + \angle C &= 180^{\circ} \\ \angle C &= 70^{\circ} \implies \color{Blue}{[90 - 70 = \boxed{20}]}
\end{align}\]
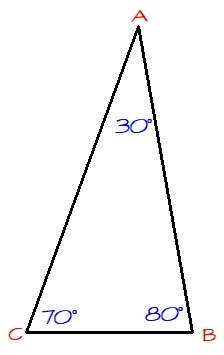 ∠
A
C
B
=
1
8
0
−
8
0
−
3
0
=
7
0
∠
A
C
B
=
1
8
0
−
8
0
−
3
0
=
7
0
The sum of complimentary angles is 9 0 ∘ . So the complement of ∠ A C B is 9 0 − 7 0 = 2 0
Let the measure of ∠ C be x . We know that the sum of a triangle's angles is 1 8 0 ∘ . We also know that the first two angles sum up to 1 1 0 ∘ . From this, the measure of ∠ C is 1 8 0 ∘ − 1 1 0 ∘ = 7 0 ∘ . The complement of an angle is 9 0 − z , where z is the measure of the angle in degrees. Thus, the complement of ∠ C is 9 0 ∘ − 7 0 ∘ = 2 0 ∘ .