As Easy As Phi
A A + B = B A = X
If A and B are positive, what is the value of X ?
The answer is 1.618.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Your solution is correct but there is a typo in your final answer.
A B + B 2 − A 2 = 0 . . . s o l v i n g f o r B , B = 2 − A ± A 2 + 4 A 2 ∴ X = B A = 1 ± 5 2 = 1 . 6 1 8 o r − . 6 1 8 .
Actually, a quick observation that the equation of X given here is itself the definition of the golden ratio ( ϕ ) gives us the the answer X = ϕ = 2 1 + 5 . The value X = 2 1 − 5 is a solution to this equation, but the author of the problem wanted people to solve this orally using the definition of golden ratio and as such specified the positive answer.
Note that X = 2 1 − 5 = ϕ − 1 = ϕ and the problem should be rephrased as "Both A and B are numbers having the same sign" so as to clear the ambiguity of people answering the negative solution.
A A + B = B A
A 2 − A B − B 2 = 0
( A 2 − 2 B ) 2 = 2 5 B 2
A − 2 B = B 2 5
B A = 2 1 + 5
X = B A = 2 1 + 5
X ≈ 1 . 6 1 8
a a + b = 1 + a b = 1 + ( b a ) − 1 = b a
( b a ) 2 − b a − 1 = 0
x = a/b = 2 1 ± 5 , reject the negative solution because that implies one of a or b are negative
We apply this rule
b a = d c = b + d a + c
Substituting a = A + B , b = A , c = A , d = B
A A + B = B A = A + B 2 A + B = 1 + A + B A = 1 + X 1 = X
⇔ X 2 − X − 1 = 0
Solving for X, taking only the positive root as A , B > 0
⇒ X = 2 1 + 5
X ≈ 1 . 6 1 8
(x+1)/x = x, so we have quadratic eqs. x^2 - x - 1 = 0, and the solution is x=1.618
x=-0.618 is also a right answer.
Log in to reply
Remember that A , B > 0 , so the negative root is not possible.
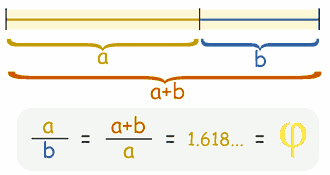
A A + B = X
A + B = A X
B = A X − A
B A = X
B = X A
A X − A = X A
A X 2 − A X = A
A X 2 − A X − A = 0
A ( X 2 − X − 1 ) = 0
Since A = 0 , hence:
X 2 − X − 1 = 0
Solve for X we get:
X = 0 . 6 1 8 or X = − 0 . 6 1 8