Calculus 4: Function

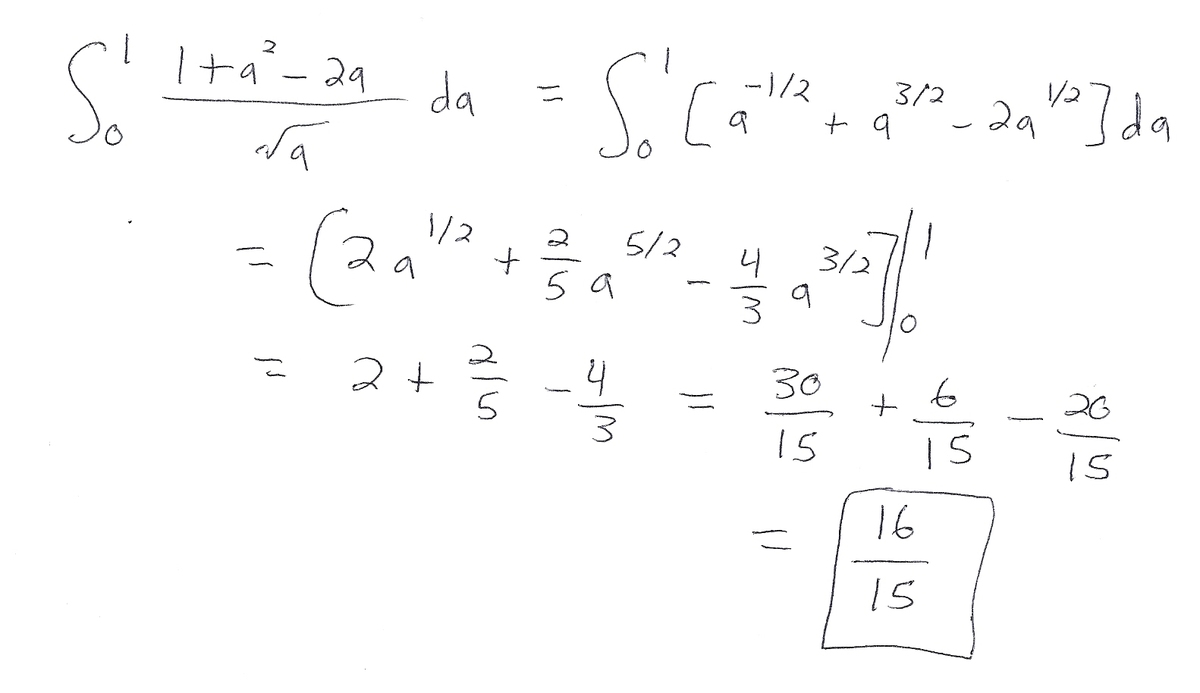
Relevant wiki: Beta Function

$\displaystyle I = \int_0^1 \dfrac{1+a^2-2a}{\sqrt[]{a}} ~ da \\ \displaystyle = \int_0^1 a^{-\frac{1}{2}} \cdot (1-a)^2 ~~ \color{#3D99F6}{\boxed{\text{rewrite the integral}}} \\ \displaystyle = \int_0^1 a^{\frac{1}{2} - 1} \cdot (1-a)^{3-1} \\ \displaystyle = \int_0^1 a^{p-1} \cdot (1-a)^{q-1} ~~ \color{#3D99F6}{\boxed{\text{ where p = }\dfrac{1}{2} \text{ and q = 3}}} \\ \displaystyle \text{Now, the above is of the form : } \int_0^1 t^{y-1}(1-t)^{x-1} \, dt \\ \displaystyle \text{Therefore, } \int_0^1 t^{y-1}(1-t)^{x-1} \, dt = B(x, y) \text{; B(x, y) represents Beta function} \\ \displaystyle \therefore I = B(p, q) = B\left(\dfrac{1}{2}, 3\right) \\ \displaystyle I = \dfrac{\Gamma\left(p\right)\Gamma\left(q\right)}{\Gamma\left(p+q\right)} \\ \displaystyle ~~ = \dfrac{\Gamma\left(\dfrac{1}{2}\right)\Gamma\left(3\right)}{\Gamma\left(\dfrac{1}{2}+3\right)} \\ \displaystyle ~~ = \dfrac{\Gamma\left(\dfrac{1}{2}\right)\Gamma\left(3\right)}{\Gamma\left(\dfrac{7}{2}\right)} \\ \displaystyle ~~ = \dfrac{\sqrt[]{\pi}\cdot2}{\dfrac{15\sqrt[]{\pi}}{8}} \\ \displaystyle ~~ = \dfrac{16}{15} \\ \displaystyle ~~ = \dfrac{A}{B} \\ \displaystyle \boxed{\therefore A-B = 16 - 15 = 1}$

$\text{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}$

Now, finding values of Gamma functions.

$\Gamma\left(\frac{1}{2}\right)=\intop_{t=0}^{+\infty}t^{\frac{1}{2}-1}e^{-t}dt=\intop_{t=0}^{+\infty}\frac{e^{-t}}{\sqrt{t}}dt, \\ y = \sqrt[]{t}; dy=\frac{dt}{2\sqrt{t}} \\ \Gamma\left(\frac{1}{2}\right)=2\intop_{y=0}^{+\infty}e^{-y^{2}}dy=\intop_{y=-\infty}^{+\infty}e^{-y^{2}}dy=\sqrt{\pi}. \\ \Gamma\left(x+1\right) = x\Gamma\left(x\right) \\ \text{For x =} \dfrac{5}{2} \\ \Gamma\left(\dfrac{7}{2}\right) = \dfrac{5}{2}\Gamma\left(\dfrac{5}{2}\right) \\ \text{For x = 3}\\ \Gamma\left(\dfrac{5}{2}\right) = \dfrac{3}{2}\Gamma\left(\dfrac{3}{2}\right) \\ \Gamma\left(\dfrac{n}{2}\right) = \dfrac{(n-2)!!\sqrt[]{\pi}}{2^{\frac{(n-1)}{2}}} \\ \Gamma\left(\dfrac{3}{2}\right) = \dfrac{(1)!!\sqrt[]{\pi}}{2^{\frac{(2)}{2}}} \\ ~~ = \dfrac{\sqrt[]{\pi}}{2}\\ \therefore \Gamma\left(\dfrac{5}{2}\right) = \dfrac{3}{2}\Gamma\left(\dfrac{3}{2}\right) \\ ~~ = \dfrac{3\pi}{4} \\ \boxed{\therefore \Gamma\left(\dfrac{7}{2}\right) = \dfrac{5}{2}\dfrac{5}{2}\Gamma\left(\dfrac{5}{2}\right) = \dfrac{5}{2} \cdot \dfrac{3\pi}{4} = \dfrac{15\pi}{8}}$

$\begin{aligned} I & = \int_0^1 \frac {1+x^2-2x}{\sqrt x} dx \\ & = \int_0^1 \frac {(x-1)^2}{\sqrt x} dx & \small \color{#3D99F6}{\text{Let }u^2=x, \ 2u \ du = dx} \\ & = \int_0^1 \frac {2u(u^2-1)^2}u du \\ & = \int_0^1 2(u^2-1)^2 \ du \\ & = 2 \int_0^1 (u^4-2u^2+1) \ du \\ & = 2\left(\frac 15 - \frac 23 + 1 \right) \\ & = \frac {16}{15} \end{aligned}$

$\implies A - B = 16 - 15 = \boxed{1}$

It's also possible to do this in a very pedestrian way.