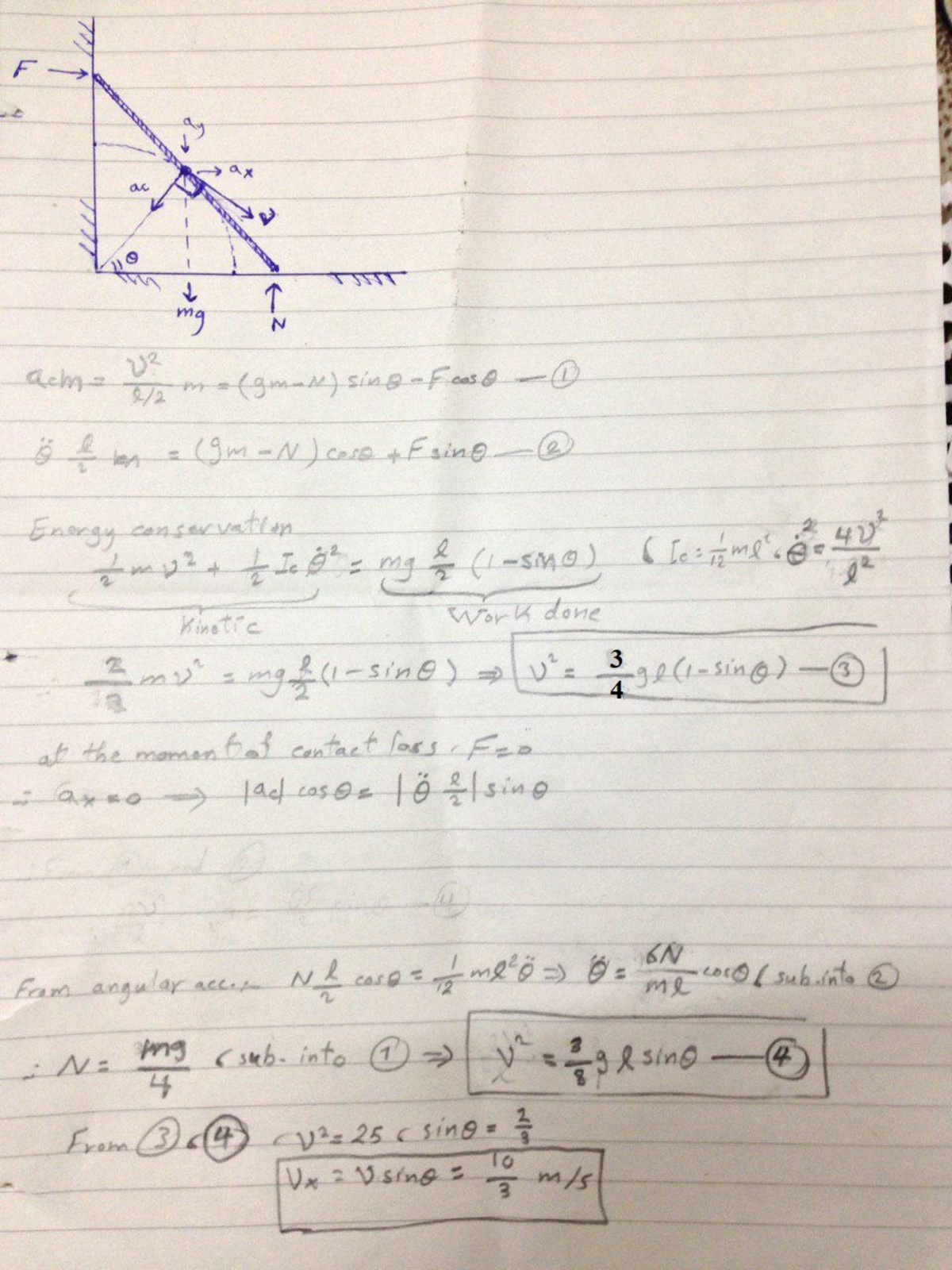Easy Complex question (part-1)
 A ladder of length l and uniform mass density stands on a frictionless floor and leans against a frictionless wall. It is initially held motionless, with its bottom end
an infinitesimal distance from the wall. It is then released, whereupon the bottom
end slides away from the wall, and the top end slides down the wall. When it loses
contact with the wall, what is the horizontal component of the velocity of the center
of mass?
Note l = 10m
Take g = 10 m/
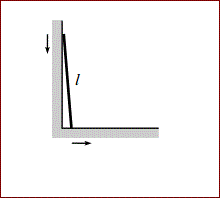
A ladder of length l and uniform mass density stands on a frictionless floor and leans against a frictionless wall. It is initially held motionless, with its bottom end
an infinitesimal distance from the wall. It is then released, whereupon the bottom
end slides away from the wall, and the top end slides down the wall. When it loses
contact with the wall, what is the horizontal component of the velocity of the center
of mass?
Note l = 10m
Take g = 10 m/
The answer is 3.333.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
I did it by the usual Newtonian way , but it can easily be done throughout Lagrangian formulation.