This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I think you have a typo on your limits of integration ( first integral limits after the change of variables should be in terms of u as well )?
Substitute 1 + x = y . Then 2 x d x = d y . At x = 0 , y = 1 and at x = 1 , y = 2 . Hence the value of the integral is 2 ( 1 − 2 1 ) = 1
Nice m8 you are really clever
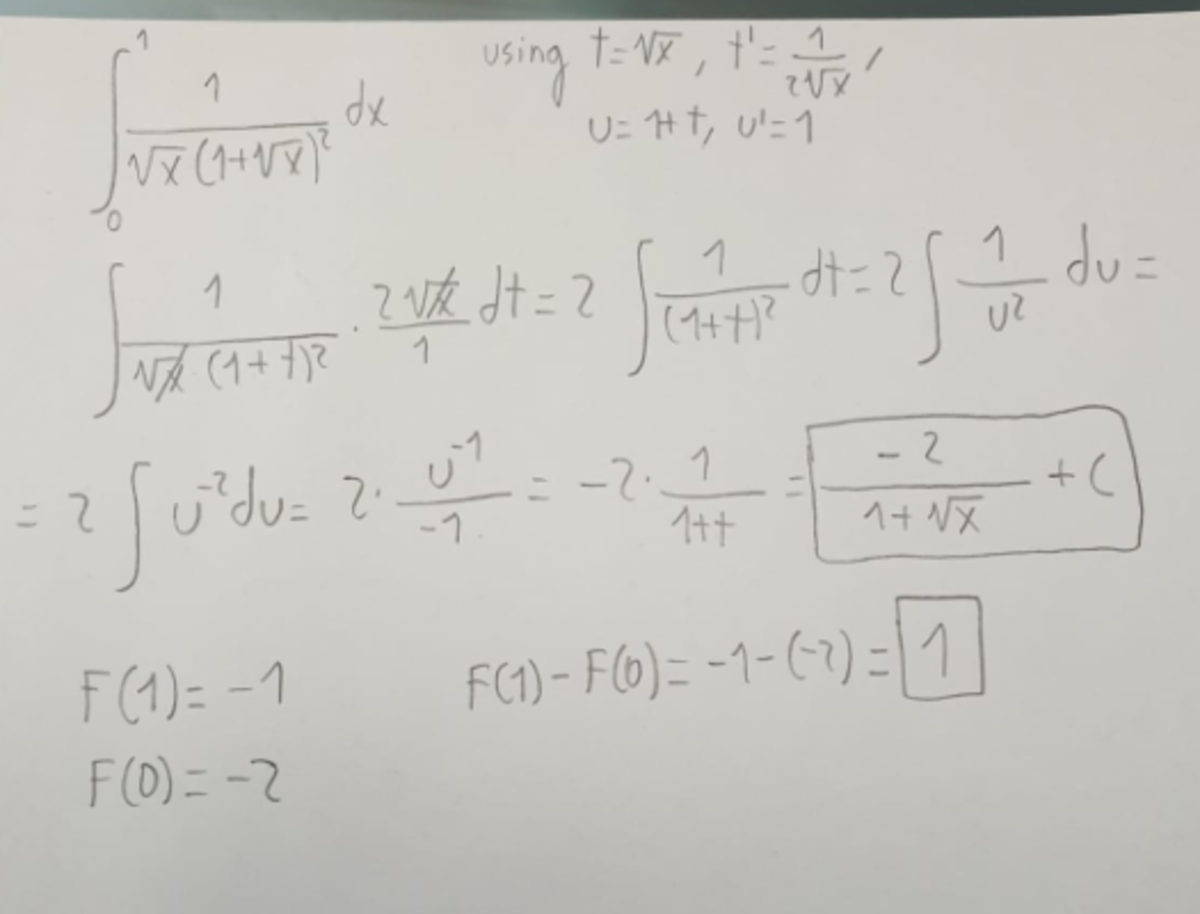
@Alak Bhattacharya's solution in LaTex
I = ∫ 0 1 x ( 1 + x ) 2 1 d x = ∫ 1 2 u 2 2 d u = − u 2 ∣ ∣ ∣ ∣ 1 2 = 1 Let u = 1 + x ⟹ d u = 2 x d x